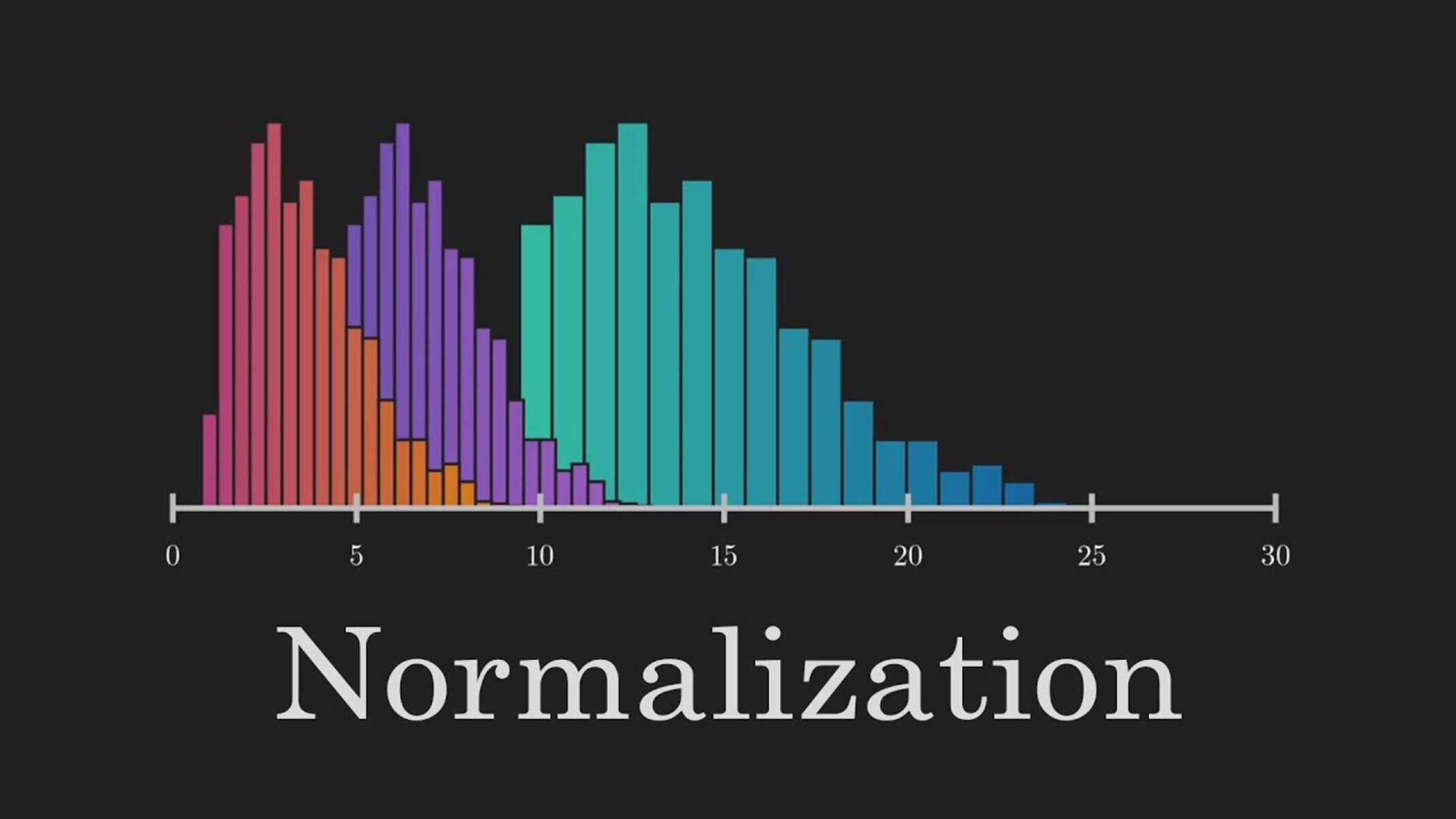
Introduction
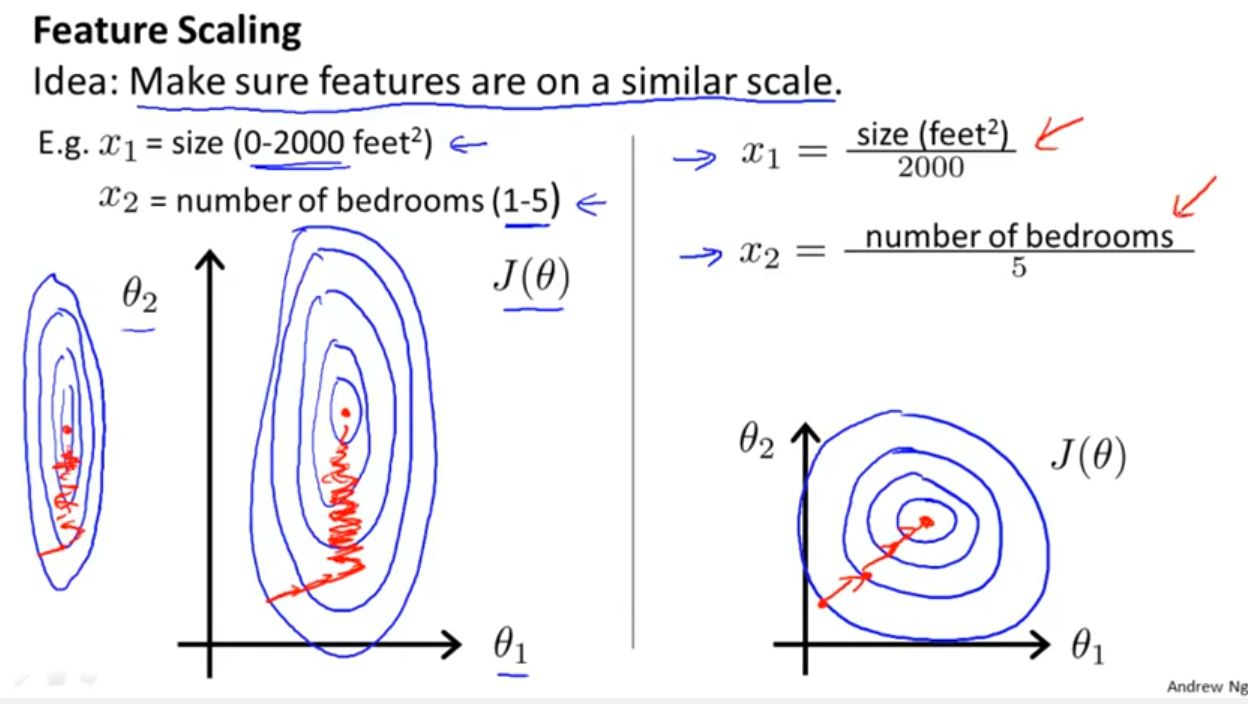
Welcome to the world of machine learning, where algorithms and data hold the power to revolutionize businesses and industries. As you dive deeper into this exciting field, you’ll discover that scaling is an essential step in the machine learning process. Scaling refers to transforming the input data to a specific range or distribution, which ensures that all features or variables are at a similar scale. In other words, scaling allows the machine learning models to handle different variables effectively and make accurate predictions.
Why is scaling important, you may wonder? Well, when the input data features have different scales, it can lead to biased results and inaccurate predictions. Machine learning algorithms often rely on various distance-based measurements, such as Euclidean distance or cosine similarity. If the features have different scales, one feature with a large range may dominate the distance calculations, rendering other features insignificant. Scaling eliminates this issue by putting all the features on a standardized scale, allowing the algorithm to focus on the underlying patterns in the data rather than the scale of the features.
There are several scaling techniques available, each with its own advantages and use cases. The choice of scaling method depends on the nature of the data and the specific requirements of the machine learning problem at hand. In this article, we will explore some common scaling techniques and discuss when to use them. By understanding the scenarios where each scaling technique shines, you can effectively preprocess your data and set the stage for optimal machine learning performance.
What is Scaling in Machine Learning?
In the realm of machine learning, scaling refers to the process of modifying the range or distribution of input data features. It involves transforming the values of different variables to a standardized scale, ensuring that all features have a similar magnitude.
Imagine you have a dataset with multiple features, each representing a different aspect of the problem you are trying to solve. These features might have vastly different ranges or units of measurement. For example, one feature could be the number of years of experience, ranging from 0 to 30, while another feature could be the annual income, ranging from a few thousand dollars to millions. The difference in scales can have a detrimental effect on machine learning algorithms that rely on numerical computations.
By scaling the features, you bring them onto a comparable scale, making it easier for the machine learning algorithms to understand the relationships between the variables. Scaling helps achieve better convergence during training and ensures that no single feature dominates the algorithm’s decision-making process based solely on its scale.
Scaling is especially crucial for algorithms that rely on distance-based calculations, such as k-nearest neighbors (KNN) and support vector machines (SVM). In these algorithms, the distance between data points plays a significant role in determining their similarity. If the features have dramatically different scales, the distances calculated may be skewed, resulting in biased predictions.
Moreover, scaling can be beneficial when using optimization algorithms like gradient descent. These algorithms often converge faster on data that is scaled properly. Without scaling, the optimization might take longer or even fail to reach the optimal solution.
Therefore, scaling is not merely a recommendation but a necessary preprocessing step in many machine learning applications. It allows for fairer comparisons and accurate predictions, ensuring the algorithms can effectively utilize the information encoded in the features.
Why is Scaling Important in Machine Learning?
Scaling plays a vital role in machine learning as it brings numerous benefits to the learning process and the performance of predictive models. Let’s explore the key reasons why scaling is crucial in machine learning.
First and foremost, scaling ensures that all features are on a level playing field. When features have significantly different scales, the impact of individual features on the overall predictions can be distorted. For instance, if one feature has a large scale compared to others, it may dominate the learning process and overshadow the contribution of other features. By scaling the features, each one can contribute proportionally to the model’s learning process, leading to a fair representation of their importance.
Another important reason to scale the data is to improve the stability and convergence of machine learning algorithms. Many algorithms are sensitive to the scale of the input data, and when the features have disparate ranges, it can hinder the convergence of the optimization process. Scaling the data helps to mitigate this issue by bringing the features to a similar scale, which facilitates the optimization process and allows the algorithms to converge more reliably and efficiently.
Scaling is particularly crucial for distance-based algorithms such as KNN or SVM. These algorithms rely on calculating distances between data points to make decisions. If the features have different scales, the distance calculations can be influenced disproportionately by the feature with the largest scale. This can lead to biased predictions and misinterpretation of the underlying patterns in the data. Scaling the features ensures that the distance calculations take into account all relevant features equally, resulting in more accurate and reliable predictions.
In addition to algorithmic considerations, scaling also helps to interpret the model’s coefficients or weights correctly. When features are not on a similar scale, the coefficients associated with each feature can become difficult to interpret. Scaling the features makes the coefficients more comparable, providing clearer insights into how each feature impacts the predictions and enabling better decision-making based on the model’s results.
Overall, scaling is a crucial step in machine learning preprocessing. It allows for fair and accurate comparisons between features, improves algorithm stability and convergence, enhances the interpretability of the models, and contributes to the overall reliability and performance of machine learning algorithms.
Types of Scaling Techniques
There are various scaling techniques available to transform the data into a standardized scale. The choice of scaling method depends on the characteristics of the data and the specific requirements of the machine learning problem. Let’s explore some commonly used scaling techniques:
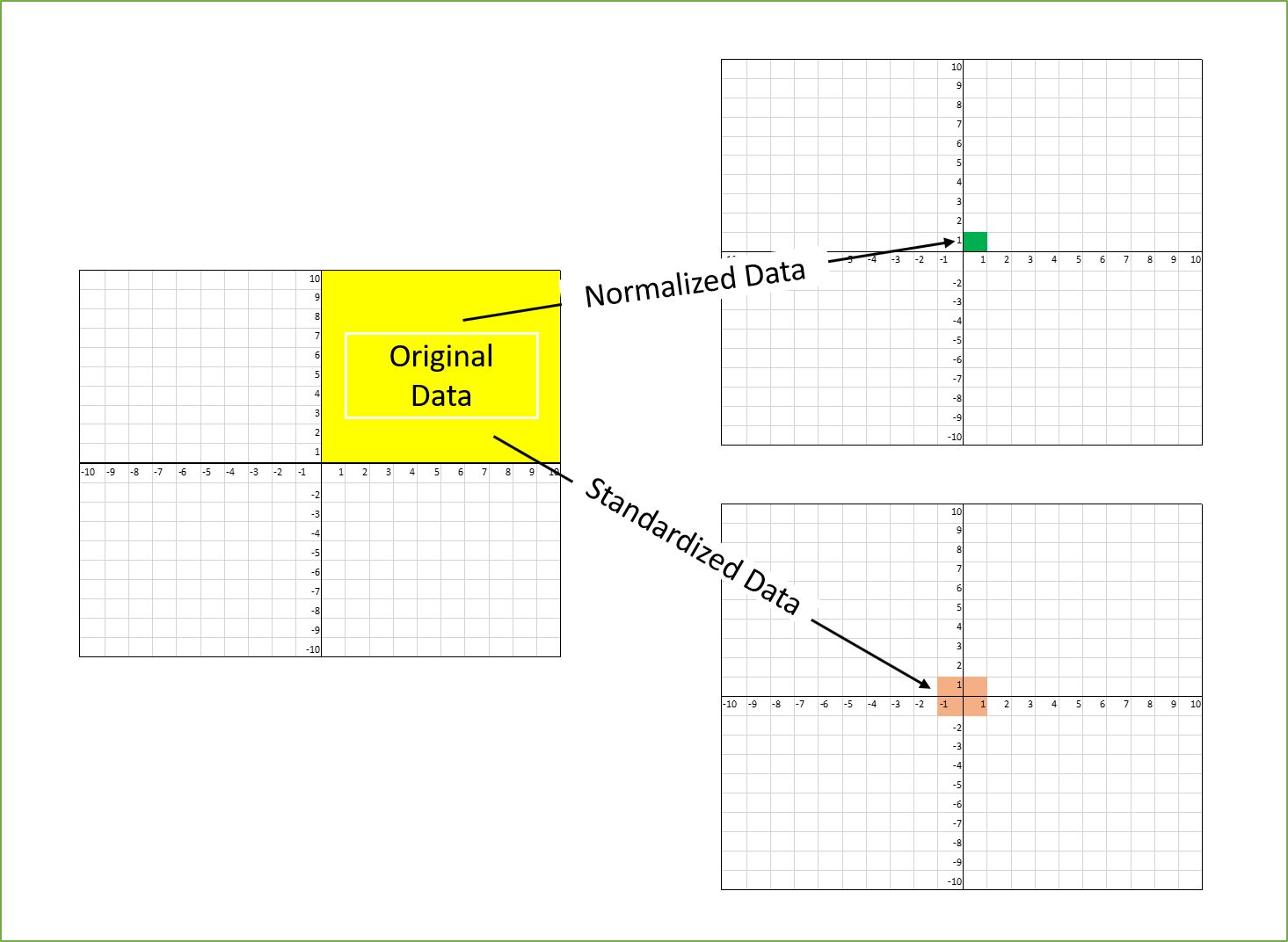
1. Min-Max Scaling: Also known as normalization, this technique scales the data to a specific range, typically between 0 and 1. It preserves the shape of the distribution while ensuring that all values are within the desired range. Min-Max scaling is suitable for features that have a bounded range and can be sensitive to outliers.
2. Standardization Scaling: This technique transforms the data to have a mean of 0 and a standard deviation of 1. It rescales the data to a standard Gaussian distribution, also known as a standard normal distribution. Standardization is useful when the data does not have a bound range and can handle outliers better than Min-Max scaling.
3. Max Absolute Scaling: In this technique, the data is scaled by the absolute maximum value of each feature. It brings the values within the range of -1 to 1 while maintaining the sign of the values. Max Absolute scaling is beneficial when the distribution of the data is skewed and contains outliers, as it retains the data’s information without distorting it.
4. Robust Scaling: This technique is robust to outliers and variations in the data distribution. It scales the features to have a median of 0 and a predefined interquartile range (IQR). Robust scaling is suitable when the data contains outliers or extreme values that can significantly impact the mean and standard deviation used in other scaling techniques.
5. Logarithmic Scaling: This technique applies a logarithmic transformation to the data. It is useful when the data is highly skewed or has a wide range of values. Logarithmic scaling helps to compress the values and make them more interpretable and normalized.
These are just a few examples of scaling techniques commonly used in machine learning. It is essential to consider the characteristics of the data and the specific requirements of the problem to choose the most appropriate scaling method. Experimenting with different techniques and evaluating their impact on the model’s performance can help in finding the optimal scaling approach for a given machine learning task.
Scenario 1: When to Use Min-Max Scaling
Min-Max scaling, also known as normalization, is a useful technique when the data features have a known and meaningful range. It scales the data to a specific range, typically between 0 and 1. Here are a few scenarios where Min-Max scaling is particularly beneficial:
- Data with bounded range: Min-Max scaling is suitable when the values of the features are confined within a specific range. For example, when dealing with features that represent percentages, scores, or rankings, the range of values is naturally bounded between 0 and 100. In such cases, applying Min-Max scaling ensures that all features are on a comparable scale.
- Normalization for interpretation: Min-Max scaling can be valuable when interpreting the results of the analysis. By scaling the features between 0 and 1, the relative importance and contribution of each feature become more apparent. This makes it easier to interpret the coefficients or weights associated with each feature and identify their impact on the predictions. It helps in understanding the relative influence of different features in the model.
- Sensitive to outliers: Min-Max scaling is less affected by outliers compared to other scaling techniques such as Standardization scaling. When outliers are present in the data, they can heavily influence the mean and standard deviation used in Standardization scaling. Min-Max scaling, on the other hand, preserves the distribution and is less affected by extreme values, making it a suitable choice in scenarios with outliers.
It’s important to note that Min-Max scaling can be sensitive to the presence of outliers within the specific range of the data. If the data contains extreme outliers, they can distort the scaling and compress the rest of the values. In such cases, it may be advisable to consider alternative scaling techniques that are more robust to outliers, such as Robust scaling or Max Absolute scaling.
In summary, Min-Max scaling is ideal for data with a bounded range, when interpreting the results of the analysis, and when the data is sensitive to outliers. By applying Min-Max scaling, you can ensure that the features are on a comparable scale and enable better interpretation and analysis of the data.
Scenario 2: When to Use Standardization Scaling
Standardization scaling, also known as Z-score normalization, is a widely used technique in machine learning. It transforms the data to have a mean of 0 and a standard deviation of 1, resulting in a standard Gaussian distribution. Here are a few scenarios where Standardization scaling is particularly useful:
- Data without a known range: Standardization scaling is advantageous when the data does not have a predefined or meaningful range. Unlike Min-Max scaling, which requires a bounded range, Standardization scaling can handle data with arbitrary or unbounded values. It brings the data onto a standardized scale, making it easier for algorithms to compare and interpret the features.
- Handling outliers: Standardization scaling is robust to outliers in the data. Outliers, which are extreme values that differ significantly from the rest of the data, can heavily influence the mean and standard deviation used in scaling techniques. Standardization looks at the distribution of the data in terms of standard deviations, making it less affected by outliers compared to other techniques. It helps ensure that the features are scaled appropriately and the algorithms are not disproportionately influenced by outliers.
- Algorithmic requirements: Some machine learning algorithms, such as logistic regression and support vector machines, assume that the features are normally distributed and have a mean of 0 and a standard deviation of 1. Applying Standardization scaling allows these algorithms to work optimally and often leads to better convergence and performance.
Standardization scaling is also useful when comparing features that have different units of measurement or scales. By bringing all features to a standardized scale, it becomes easier to identify and analyze the relative magnitudes and effects of each feature on the predictions.
However, it’s important to note that Standardization does not bound the data to a specific range like Min-Max scaling. Thus, if the range of the data is important or meaningful, Min-Max scaling might be more appropriate. Additionally, certain algorithms and models may not require or benefit from the standardization of the features. In such cases, it’s important to understand the specific requirements and constraints of the problem at hand.
In summary, Standardization scaling is useful when dealing with data without a known range, when handling outliers, and when the algorithmic requirements or assumptions favor normally distributed features. By applying Standardization scaling, you can standardize the features, handle outliers effectively, and enhance the performance of your machine learning models.
Scenario 3: When to Use Max Absolute Scaling
Max Absolute scaling is a scaling technique that transforms the data to a range of -1 to 1, while preserving the sign of the values. It is particularly suitable in scenarios where the distribution of the data is skewed or when outliers are present. Let’s explore some scenarios where Max Absolute scaling is beneficial:
- Data with skewed distribution: When the data is heavily skewed, meaning it has a long tail on one side, Max Absolute scaling can be a useful choice. Skewed data can affect the performance of machine learning models and make it difficult to capture the underlying patterns. By scaling the data to a range of -1 to 1, Max Absolute scaling helps to compress the values while preserving the information and maintaining the relationship between the features.
- Handling outliers: Max Absolute scaling is robust to outliers, similar to Robust scaling. When outliers are present in the data, they can significantly impact the mean and standard deviation used in other scaling techniques. Max Absolute scaling scales the data based on the maximum absolute value, which makes it less sensitive to outliers. It allows for the normalization of the data without distorting the relationship between variables.
- Data with asymmetric distributions: Max Absolute scaling is useful when dealing with data that exhibits asymmetric distributions. For example, in financial data, where positive and negative values represent gains and losses, Max Absolute scaling ensures that both positive and negative values are scaled within the range of -1 to 1. This helps maintain the asymmetry of the data and preserves the significance of both positive and negative values.
It is important to note that Max Absolute scaling does not consider the mean or the standard deviation of the data, unlike other scaling techniques. Therefore, it may not be suitable for data where the mean and standard deviation are essential for interpretation or normalization.
In summary, Max Absolute scaling is beneficial in scenarios where the data has a skewed distribution, when outliers are present, and when dealing with data that exhibits asymmetric distributions. By applying Max Absolute scaling, you can compress the data values while preserving the information and maintaining relative differences between the features, enhancing the performance of your machine learning models.
Scenario 4: When to Use Robust Scaling
Robust scaling is a robust normalization technique that is particularly useful when dealing with data that contains outliers or is not normally distributed. It scales the data by centering it around the median and scaling it based on the predefined interquartile range (IQR). Here are a few scenarios where Robust scaling is beneficial:
- Data with outliers: When the data contains outliers that can significantly affect the mean and standard deviation used in other scaling techniques, Robust scaling becomes a suitable choice. It utilizes the median and IQR instead of the mean and standard deviation, making it more resistant to the influence of outliers. By centering the data around the median rather than the mean, Robust scaling provides a more reliable measure of central tendency.
- Data with non-normal distribution: Standardization scaling assumes that the data features are normally distributed. However, if the data has a non-normal distribution, such as a skewed or heavy-tailed distribution, Robust scaling is a better option. It eliminates the need for normally distributed features and ensures that the scaling is robust to deviations from normality. It brings the data onto a standardized scale while preserving the distributional characteristics of the data.
- Handling variables of different scales: Robust scaling is beneficial when dealing with datasets that have features with varying scales. For instance, if the dataset contains features that have different units of measurement or different orders of magnitude, Robust scaling can effectively bring all the features to a comparable scale. By normalizing the data based on the IQR, it ensures that the scaling is relative to the spread of the data rather than the absolute values.
It is important to note that Robust scaling is less affected by outliers, but it does not completely remove their influence. In extreme cases, where the outliers are very extreme compared to the rest of the data, other techniques such as trimming or removal of outliers may need to be performed in addition to Robust scaling.
In summary, Robust scaling is suitable when dealing with data that contains outliers, has non-normal distributions, or has features with different scales. By applying Robust scaling, you can center the data around the median, normalize it using the IQR, and achieve a scaling technique that is robust to outliers and deviations from normality.
Scenario 5: When to Use Logarithmic Scaling
Logarithmic scaling is a useful technique when dealing with data that is highly skewed or has a wide range of values. It applies a logarithmic transformation to the data, compressing the values and making them more interpretable. Here are a few scenarios where logarithmic scaling is particularly beneficial:
- Skewed data: Logarithmic scaling is effective when the data has a highly skewed distribution, meaning it has a long tail on one side. By applying a logarithmic transformation, the extreme values are compressed, and the values towards the lower end of the distribution are expanded. This makes the overall distribution more symmetrical and can help to better capture the underlying patterns in the data.
- Wide range of values: When the data has a wide range of values that span several orders of magnitude, logarithmic scaling can bring the values onto a more manageable scale. It compresses the values, making them more uniformly distributed and reducing the impact of extreme values on the analysis. This is particularly useful for data analysis and visualization, as it allows for better data interpretation and comparison.
- Data with multiplicative trends: Logarithmic scaling is useful when analyzing data that exhibits multiplicative trends rather than additive trends. For example, in financial data, where percentage changes or growth rates are more meaningful than absolute changes, logarithmic scaling can transform the data into a more linear relationship, making it easier to identify patterns and trends.
It’s important to note that logarithmic scaling is suitable for positive data values only, as taking the logarithm of non-positive values is undefined. Additionally, the interpretation of features after logarithmic scaling should consider that the transformed values are no longer on the original scale but rather on a logarithmic scale.
In summary, logarithmic scaling is beneficial when dealing with highly skewed data, a wide range of values, or data with multiplicative trends. By applying a logarithmic transformation, you can compress the values, improve the symmetry of the distribution, and enhance the interpretability and analysis of the data.
Conclusion
Scaling is a critical step in the machine learning process that ensures the input data features are on a comparable scale, allowing algorithms to make accurate predictions and uncover meaningful patterns. In this article, we have explored various scaling techniques and discussed the scenarios where each technique shines.
Min-Max scaling, or normalization, is suitable for data with a bounded range and when the interpretation of results is important. It brings the features within the range of 0 to 1, making it easier to compare their relative importance.
Standardization scaling, or Z-score normalization, is beneficial when dealing with data without a known range, handling outliers, or when algorithmic requirements favor normally distributed features. It brings the features to a mean of 0 and a standard deviation of 1, ensuring fair comparisons and better convergence.
Max Absolute scaling is advantageous for skewed data, data with extreme values or outliers, and asymmetric distributions. It compresses the values within the range of -1 to 1, preserving the sign of the data and enabling robust scaling.
Robust scaling is useful when the data contains outliers or does not follow a normal distribution. It scales the features based on the median and the interquartile range, making it resistant to the influence of extreme values and ensuring relative scaling.
Logarithmic scaling is particularly suitable for highly skewed data, wide ranges of values, or data with multiplicative trends. It compresses the values and makes the distribution more symmetrical, facilitating better analysis and interpretation.
Choosing the appropriate scaling technique depends on the characteristics of the data and the specific requirements of the problem at hand. It is essential to consider the distribution of the data, the presence of outliers, the interpretability of the results, and the assumptions of the algorithms being used.
By understanding the different scenarios where each scaling technique excels, you can preprocess your data effectively and set the stage for optimal machine learning performance. Scaling empowers models to make accurate predictions, enhances algorithm stability, and provides interpretability, ultimately leading to more reliable and actionable insights from your machine learning endeavors.