Introduction
Welcome to the exciting world of machine learning! In this article, we will explore the concept of a weight vector and its significance in machine learning algorithms. As you delve into the field of machine learning, understanding the role of a weight vector will be crucial for developing accurate and efficient models.
Machine learning involves training models to learn patterns and make predictions based on available data. These models rely on numerical weights assigned to the features of the data, helping them differentiate between different classes or make accurate predictions. This is where the weight vector comes into play.
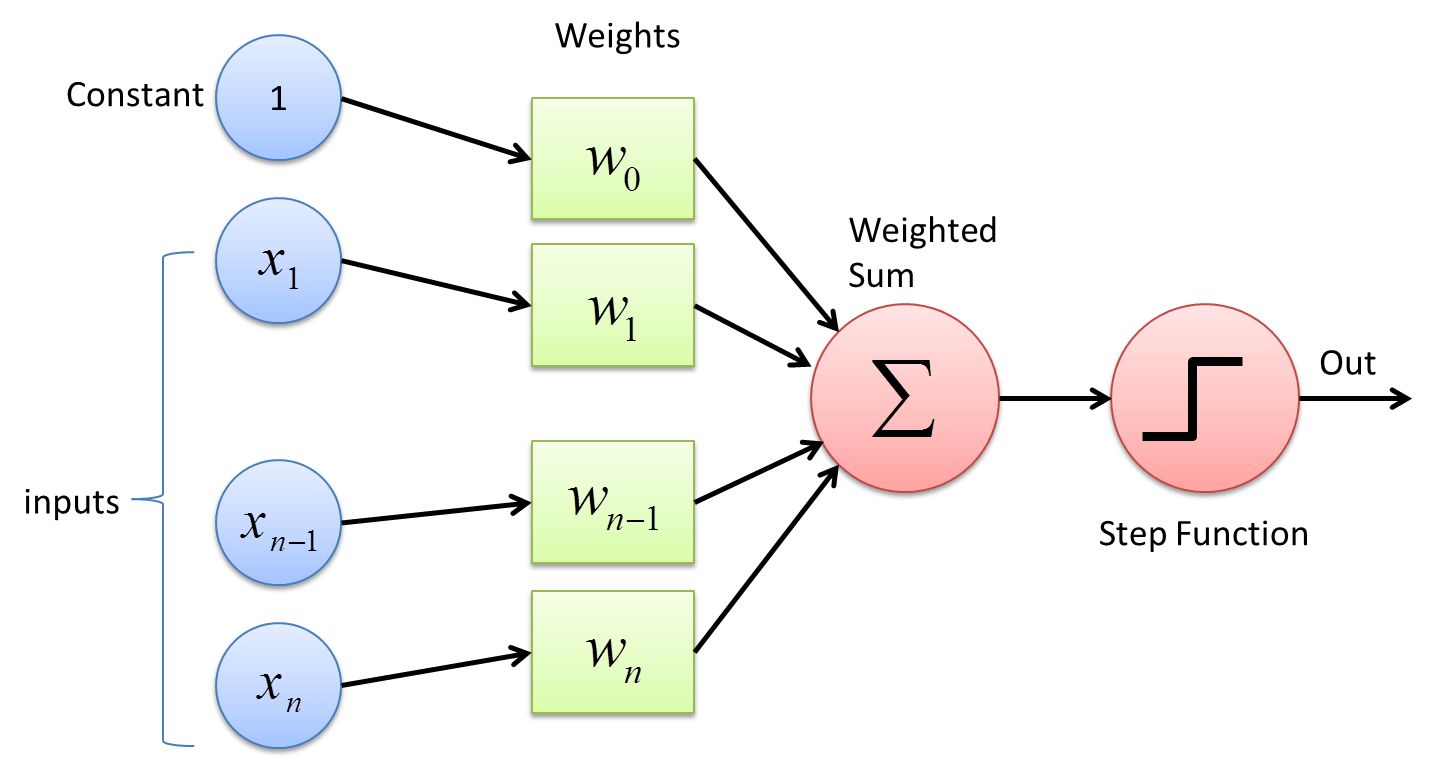
A weight vector, also known as a weight matrix or coefficient vector, is a multidimensional vector consisting of numerical values that determine the importance of each feature in a machine learning algorithm. These weights are adjusted during the training process, allowing the algorithm to assign more significance to certain features and less to others.
The importance of the weight vector lies in its ability to influence the overall behavior and performance of the machine learning model. By assigning appropriate weights to the features, the algorithm can focus on relevant information and make more accurate predictions. The weight vector essentially acts as a set of guidelines that guide the learning process and shape the behavior of the model.
Understanding the concept of a weight vector is crucial because it directly impacts the accuracy and reliability of the machine learning model. By assigning appropriate weights, the model can learn to identify important patterns and make reliable predictions, while minimizing errors.
In the following sections, we will delve into more detail about how weight vectors are utilized in machine learning algorithms, the common algorithms that employ weight vectors, and how to calculate and optimize weight vectors for better model performance.
Definition of Weight Vector in Machine Learning
In machine learning, a weight vector is a mathematical representation that assigns importance to different features or attributes of a dataset. It is a multidimensional vector that contains numerical values corresponding to each feature, indicating the weight or significance of that feature in the learning process.
The weight vector acts as a set of coefficients that influence the contribution of each feature to the final output of a machine learning algorithm. By adjusting the weights, the algorithm can focus on the most influential features and disregard or downplay less important ones.
To illustrate this concept, let’s consider a simple example. Suppose we have a machine learning algorithm that predicts housing prices based on features like the number of bedrooms, square footage, and location. The weight vector associated with this algorithm would assign numerical values to each of these features, indicating their relative importance.
For instance, if the weight vector assigns a higher value to the number of bedrooms, it implies that the number of bedrooms has a more significant impact on the final price prediction. On the other hand, if the weight vector assigns a lower value to the square footage, it suggests that square footage has a comparatively lesser influence on the predicted housing price.
The weight vector is typically initialized randomly and adjusted through an iterative process during the training phase of the machine learning algorithm. The adjustment of weights is based on the algorithm’s optimization objective, which could involve minimizing the prediction error, maximizing the accuracy, or achieving some other desired outcome.
By fine-tuning the weight vector, the machine learning algorithm can learn the underlying patterns and relationships in the data, leading to improved predictions or classifications. The weight vector essentially guides the algorithm in determining the importance of different features, enabling it to weigh the evidence from each feature appropriately.
It is worth noting that the weight vector can also incorporate a bias term, which accounts for any systematic bias in the data. The bias term represents a constant value that helps the model account for factors that cannot be directly captured by the input features.
Overall, the weight vector is a fundamental component of many machine learning algorithms, playing a critical role in determining how features contribute to the final output. By adjusting and optimizing the weights, machine learning models can learn and generalize from data, making accurate predictions or classifications.
Importance of Weight Vector
The weight vector is of utmost importance in machine learning as it determines the significance of each feature in the learning process. Here are some key reasons why the weight vector is crucial:
1. Feature Importance: The weight vector allows the machine learning algorithm to assign different degrees of importance to each feature. By adjusting the weights, the algorithm can emphasize relevant features that have a strong impact on the output and downplay less influential ones. This helps in better understanding the underlying patterns and relationships in the data.
2. Model Flexibility: The weight vector provides flexibility in the machine learning model. By adjusting the weights, the model can adapt to different datasets and make predictions or classifications based on unique patterns. This flexibility allows the model to generalize well and perform accurately on unseen data.
3. Interpretability: The weight vector also provides interpretability to the model. By examining the weights assigned to each feature, we can gain insights into which features are the most influential in making predictions or classifications. This knowledge is essential for understanding the inner workings of the model and validating its decision-making process.
4. Model Optimization: The weight vector plays a crucial role in optimizing the machine learning model. During the training phase, the weights are adjusted iteratively to minimize the prediction error or maximize the desired performance metric. This optimization process ensures that the model learns the most relevant information from the data and makes accurate predictions or classifications.
5. Overfitting Prevention: The weight vector helps prevent overfitting, which is a common issue in machine learning. Overfitting occurs when a model performs exceptionally well on the training data but fails to generalize to new, unseen data. By regularizing the weights and incorporating regularization techniques, the model can avoid overemphasizing noisy or irrelevant features, thereby improving its generalization capabilities.
Overall, the weight vector is vital for fine-tuning the machine learning model, understanding feature importance, optimizing performance, and preventing overfitting. It empowers the model to learn from data, make accurate predictions or classifications, and uncover meaningful insights in complex datasets.
How Weight Vector is Used in Machine Learning Algorithms
The weight vector plays a crucial role in numerous machine learning algorithms, influencing their behavior and enabling accurate predictions or classifications. Here are some common ways in which the weight vector is utilized:
1. Linear Models: In linear regression and linear classification algorithms, the weight vector determines the coefficients for each feature. The linear model computes the weighted sum of the features, and the weight vector dictates how much each feature contributes to the final output. By adjusting the weights, the model can find the best line or hyperplane that fits the data, allowing for effective prediction or classification.
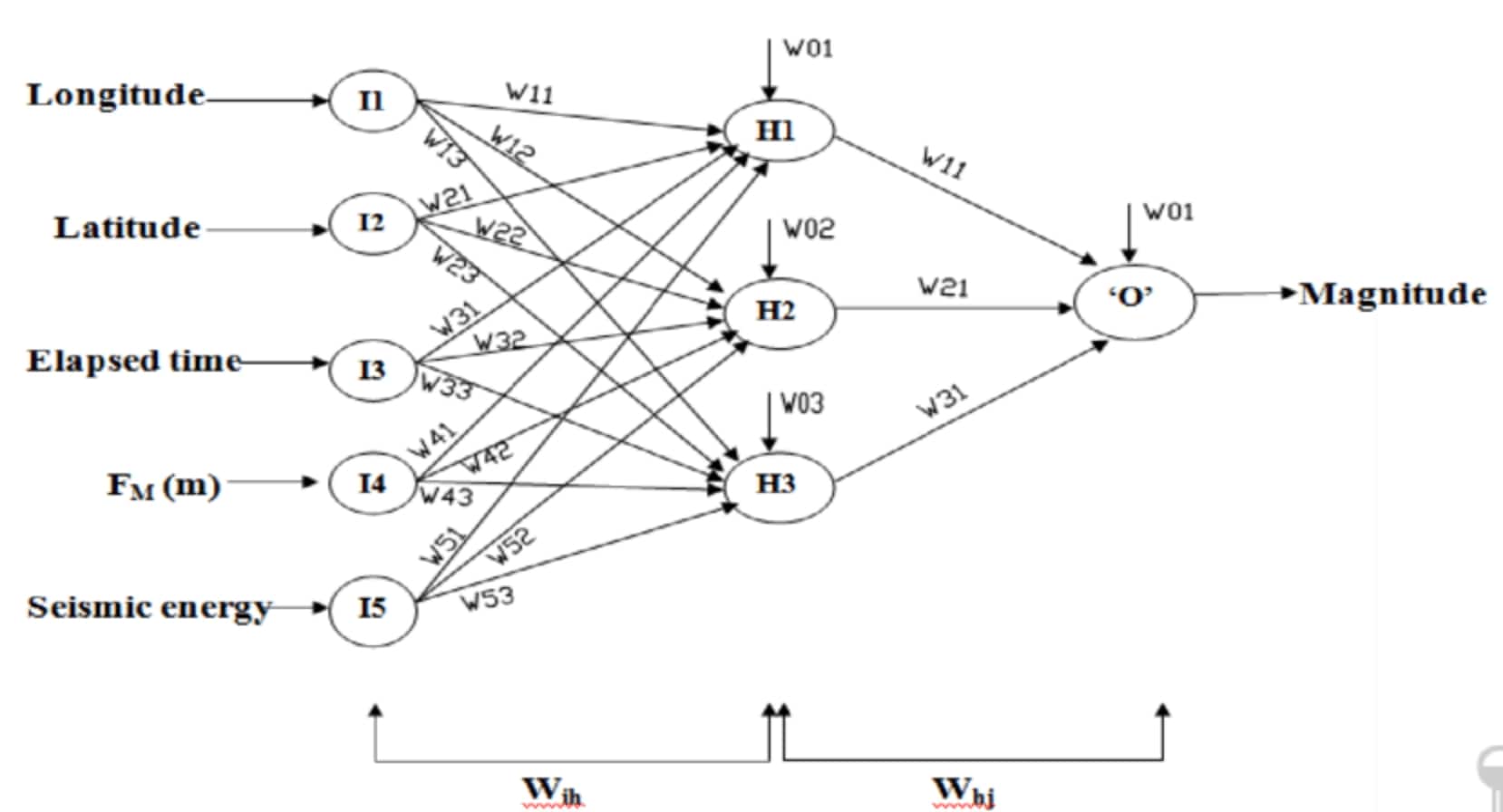
2. Neural Networks: In neural network architectures, the weight vector connects the layers of neurons. Each connection between two neurons has a corresponding weight, which determines the strength of the connection. The weight vector is adjusted through backpropagation, where the network learns from the errors and updates the weights accordingly. The weights in the neuron connections enable the network to learn complex representations and make accurate predictions.
3. Support Vector Machines (SVM): In SVM algorithms, the weight vector defines the separating hyperplane between different classes. It determines the orientation and position of the hyperplane, which maximizes the margin between the classes. The weight vector is adjusted to find the optimal hyperplane that separates the data points, allowing for effective classification.
4. Decision Trees and Random Forests: In decision tree-based algorithms, the weight vector influences the feature selection process at each split. The algorithm determines the most informative feature by evaluating the weight of each feature. In random forests, the weight vector is used in the ensemble of decision trees, guiding the combination of predictions from individual trees to make the final prediction or classification.
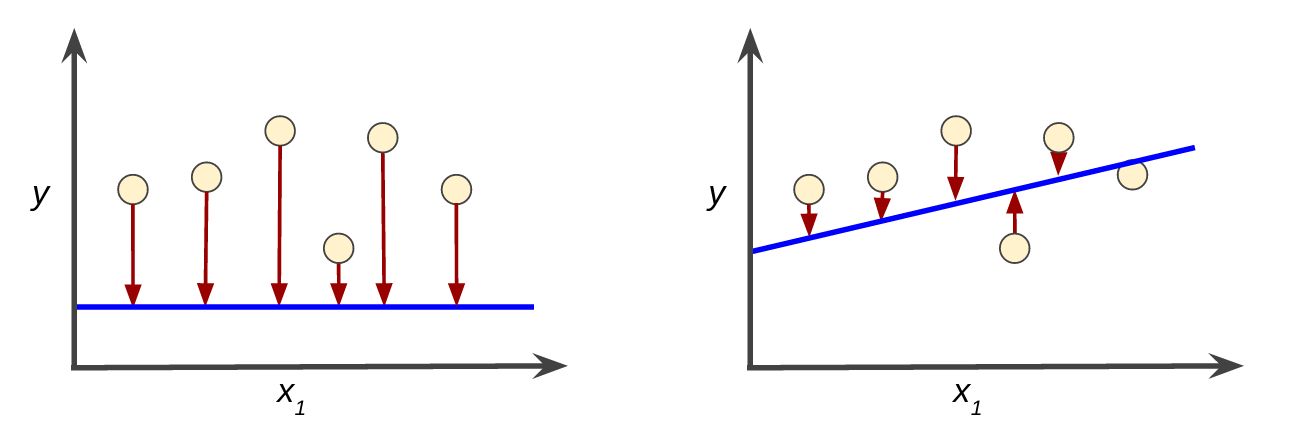
5. Gradient Descent: In optimization algorithms such as gradient descent, the weight vector is adjusted iteratively to minimize the loss function. The algorithm computes the gradients of the loss function with respect to the weights and updates them in the direction that reduces the loss. By adjusting the weight vector, the algorithm converges towards the optimal set of weights that minimizes the loss and improves the model’s performance.
These are just a few examples of how the weight vector is used in machine learning algorithms. The weight vector provides the algorithms with the necessary information to learn from the data and make accurate predictions or classifications. By adjusting the weights, these algorithms can optimize their performance, generalize well, and adapt to different datasets.
Common Machine Learning Algorithms that Utilize Weight Vector
Various machine learning algorithms rely on weight vectors to make predictions, classify data, and optimize their performance. Here are some of the most common algorithms that utilize weight vectors:
1. Logistic Regression: Logistic regression is a popular algorithm for binary classification, and it uses a weight vector to determine the importance of each feature in making predictions. The weight vector is adjusted through gradient descent or other optimization techniques, allowing the algorithm to find the best decision boundary that separates the two classes.
2. Support Vector Machines (SVM): SVM algorithms aim to find the optimal hyperplane that separates data points belonging to different classes. The weight vector in SVMs determines the orientation and position of the hyperplane. It is adjusted to maximize the margin between the classes, increasing the generalization capability of the algorithm.
3. Neural Networks: Neural networks consist of layers of interconnected neurons, and the weights in the connections between neurons form the weight vector. The weight vector determines the strength of the connections and influences the computations within the network. Training a neural network involves adjusting the weight vector through backpropagation to minimize the error between the predicted and actual outputs.
4. Linear Regression: Linear regression is a commonly used algorithm for regression tasks. It uses a weight vector to assign importance to the features and calculate the predicted output based on the weighted sum of the features. By adjusting the weights, linear regression seeks to find the best fit line that minimizes the prediction error.
5. Decision Trees: Decision tree-based algorithms, such as Random Forests and Gradient Boosting Machines, use a weight vector to determine the importance of each feature during the tree construction process. The weight vector guides the splitting of nodes and enables the algorithm to make decisions based on the most informative features.
6. Naive Bayes: Naive Bayes algorithms rely on a weight vector to assign probabilities to different features in a classification task. The weight vector represents the conditional probabilities of each feature given a specific class. By adjusting the weights, Naive Bayes algorithms can make accurate predictions based on the likelihood of different feature values given the observed data.
These are just a few examples of machine learning algorithms that utilize weight vectors. Each algorithm has its own way of utilizing the weight vector to make predictions, classify data, or optimize its performance. Understanding how the weight vector is utilized in different algorithms is crucial for selecting the appropriate algorithm for a given task and optimizing its performance.
How to Calculate Weight Vector in Machine Learning
The calculation of the weight vector in machine learning involves an optimization process that aims to find the optimal set of weights for a given learning task. The specific method for calculating the weight vector depends on the algorithm and objective of the machine learning task. Here are some general steps involved in calculating the weight vector:
1. Define a Loss Function: The first step is to define a loss function that quantifies the error between the model’s predicted output and the true output. The choice of loss function depends on the specific task, such as mean squared error for regression or cross-entropy loss for classification.
2. Choose an Optimization Algorithm: Select an optimization algorithm that helps in minimizing the loss function and finding the optimal set of weights. Common optimization algorithms include gradient descent, stochastic gradient descent, or more advanced techniques like Adam or RMSprop.
3. Initialize the Weight Vector: Initialize the weight vector with random values or specific initialization techniques depending on the algorithm. This step is important as it sets the starting point for the optimization process.
4. Iterate and Update the Weights: Start the training process by iterating over the dataset multiple times, also known as epochs. For each iteration, compute the predicted output using the current weights, calculate the loss, and then update the weights based on the optimization algorithm chosen. The goal is to minimize the loss and improve the model’s performance.
5. Termination Criterion: Define a termination criterion to stop the training process. This can be a maximum number of iterations, reaching a specific level of performance, or observing negligible improvement in the loss function. Termination criteria prevent overfitting and unnecessary computation.
6. Evaluate the Weight Vector: After the training process is complete, evaluate the performance of the model using a separate validation dataset or cross-validation techniques. Assess metrics such as accuracy, precision, recall, or mean squared error to gauge the model’s effectiveness.
7. Regularization (Optional): Depending on the algorithm and the complexity of the task, you may choose to incorporate regularization techniques such as L1 or L2 regularization. These techniques add penalty terms to the loss function, helping to avoid overfitting and control the complexity of the weight vector.
By following the steps above, the weight vector can be calculated and optimized to achieve the best performance for the specific machine learning task. It is important to note that different algorithms have different approaches to calculating the weight vector, and the specific implementation may vary accordingly. Understanding the mathematical foundations of the chosen algorithm and its optimization process can further assist in calculating the weight vector accurately.
Tips for Optimizing Weight Vector in Machine Learning
Optimizing the weight vector is crucial in achieving accurate and reliable predictions in machine learning models. Here are some tips to enhance the optimization process and improve the performance of the weight vector:
1. Feature Scaling: Consider normalizing or standardizing the input features to a similar scale before assigning weights. This can prevent certain features from dominating the weight vector due to their larger scale, ensuring that all features contribute meaningfully to the model’s predictions.
2. Regularization: Incorporate regularization techniques such as L1 or L2 regularization in the loss function to prevent overfitting. Regularization adds penalty terms to the loss function, encouraging the weight vector to be simpler and reducing the risk of memorizing noise in the training data.
3. Learning Rate: Adjust the learning rate to an appropriate value for the optimization algorithm. A high learning rate may cause the weight updates to be too large, leading to unstable convergence or overshooting the optimal weights. On the other hand, a low learning rate can slow down the optimization process. Experiment with different learning rates to find the optimal balance.
4. Batch Size: When using stochastic gradient descent or mini-batch gradient descent, consider adjusting the batch size. A smaller batch size introduces more noise into the weight updates, but can potentially converge faster. A larger batch size provides more stable updates but may require more computation. Experiment to find the batch size that best suits the dataset and optimization process.
5. Early Stopping: Implement early stopping to prevent overfitting. Monitor the performance of the model on a validation set and stop the training process when the validation performance starts to deteriorate. This prevents the weight vector from being optimized excessively for the training data at the expense of generalization.
6. Cross-Validation: Use cross-validation techniques, such as k-fold cross-validation, to evaluate the performance of the model with different sets of hyperparameters or weight vectors. This helps to ensure that the model’s performance is not influenced by the specific division of the data into training and validation sets.
7. Intrinsic Dimensionality: Consider the intrinsic dimensionality of the dataset. If the dimensionality is high and there is limited data, reducing the dimensionality through feature selection or dimensionality reduction techniques can help improve the optimization process and the performance of the weight vector.
8. Hyperparameter Tuning: Explore different hyperparameters, such as regularization strength, learning rate, or the number of iterations, to find the optimal configuration that yields the best performance. Utilize techniques like grid search or random search to systematically search the hyperparameter space.
9. Model Architecture: Evaluate different model architectures to see how they affect the optimization process and the resulting weight vector. Different architectures, activation functions, or network depths can impact the expressiveness of the model and the performance of the weight vector.
By following these tips, you can improve the optimization process and enhance the performance of the weight vector in machine learning models. Remember that optimization is an iterative process, and experimentation is key to finding the optimal configuration for a specific dataset and task.
Conclusion
The weight vector is a fundamental concept in machine learning that plays a crucial role in determining the importance of features and optimizing the performance of models. It guides the learning process, allowing algorithms to assign significance to different features and make accurate predictions or classifications.
Throughout this article, we explored the definition and importance of the weight vector in machine learning. We discovered how it is used in various algorithms, such as logistic regression, support vector machines, neural networks, and decision trees. Furthermore, we discussed the steps involved in calculating the weight vector and provided tips for optimizing its performance.
Understanding the role of the weight vector empowers us to build more accurate and efficient models. By adjusting the weights, we can focus on relevant features, prevent overfitting, and achieve better generalization. Moreover, the weight vector allows us to interpret the model’s behavior and gain insights into the underlying patterns in the data.
It is important to remember that the process of optimizing the weight vector requires careful consideration of various factors, including feature scaling, regularization, learning rate, and validation techniques. By following best practices and experimenting with different approaches, we can fine-tune the weight vector and unlock the full potential of machine learning models.
In conclusion, the weight vector is a powerful tool that empowers machine learning algorithms to make accurate predictions and classifications. It allows us to assign importance to features, optimize performance, and gain insights into the dataset. By leveraging the weight vector effectively, we can develop robust and reliable machine learning models that contribute to solving complex problems across various domains.