Introduction
Welcome to the exciting world of machine learning! In this rapidly evolving field, one crucial step in preparing data for analysis is data normalization. It is a process that ensures data is standardized and brings it within a specific range to improve the accuracy and performance of machine learning algorithms.
Data normalization involves transforming the data so that it follows a specific distribution or range. This process is essential as machine learning algorithms often require that data is presented in a consistent format, with similar scales and distributions. Failure to normalize data can lead to biased results and inaccurate predictions.
This article will delve into the concept of data normalization, explaining why it is necessary and the benefits it brings to machine learning. We will also explore common normalization techniques and discuss scenarios where normalization may not be needed.
Understanding the importance of data normalization is crucial for machine learning practitioners, as it directly impacts the quality and reliability of their models. So, let’s dive in and explore why we need to normalize data in machine learning.
What is data normalization?
Data normalization is the process of transforming data into a consistent and standardized format by adjusting its values to fit within a specific range. It is an essential step in data preprocessing, which involves cleaning, organizing, and preparing data for analysis.
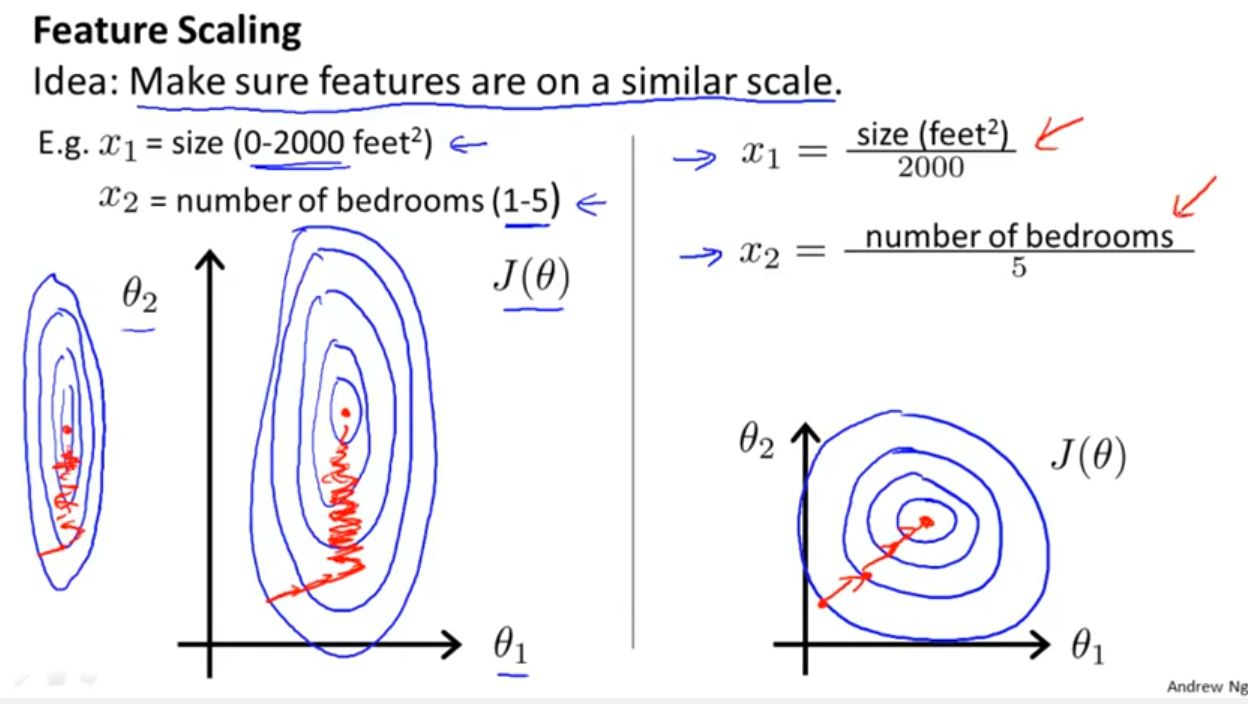
Normalization ensures that all variables in the dataset have similar scales. This is crucial because machine learning algorithms often perform poorly when working with features that have different scales. By normalizing the data, we bring all variables to a common scale, which allows algorithms to make unbiased and accurate predictions.
There are various normalization techniques available, but the underlying principle remains the same: re-scaling the data to a standard range. This range can be between 0 and 1 or -1 and 1, depending on the needs of the specific situation.
The normalization process preserves the relationships between variables while making them easier to compare and interpret. It eliminates any biases caused by the inherent differences in the scales of the input features. By doing so, it ensures that no single attribute dominates the learning process and prevents the model from being overly sensitive to certain features.
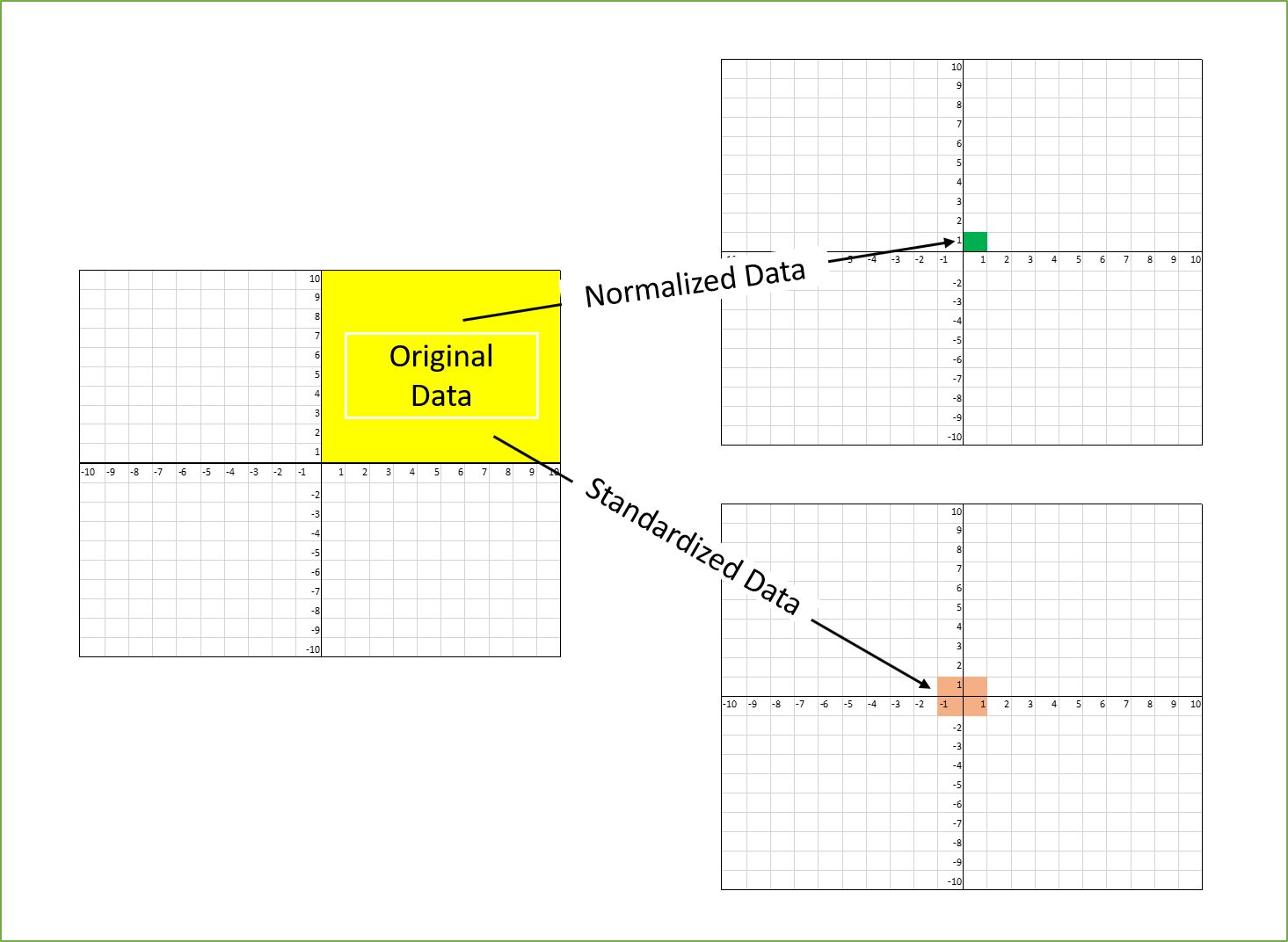
Normalization should not be confused with standardization, though they are related concepts. Normalization focuses on rescaling the data within a specific range, while standardization involves transforming the data to have a mean of 0 and a standard deviation of 1.
In summary, data normalization is a crucial step in preparing data for machine learning. By transforming data into a standardized format, it allows algorithms to perform optimally and make accurate predictions. In the next section, we will explore the reasons why we need to normalize data in machine learning.
Why do we normalize data?
Data normalization plays a pivotal role in machine learning because it brings numerous benefits to the modeling process. Let’s explore some of the key reasons why we need to normalize data:
1. Eliminating scale disparities: Machine learning algorithms often rely on numerical computations to make predictions. When features have significantly different scales, certain variables may dominate the model, leading to biased results. By normalizing the data, we ensure that all variables are on a similar scale, preventing any one attribute from overpowering the learning process.
2. Improving algorithm performance: Normalizing data can lead to significant improvements in algorithm performance. When features are brought within a specific range, models can converge more quickly, resulting in faster and more accurate predictions. Additionally, normalizing data helps algorithms to better capture patterns and relationships between variables.
3. Facilitating feature comparison: Normalization makes it easier to compare and interpret the values of different features. With all variables on the same scale, it becomes simpler to identify trends, spot outliers, and understand the relative importance of each attribute in the data.
4. Enhancing model interpretation: Normalization aids in the interpretability of machine learning models. When variables are transformed to a common scale, the coefficients or weights assigned to each feature become more meaningful and can be directly compared. This allows us to interpret the impact of each feature on the model’s predictions.
5. Enabling efficient gradient descent: Gradient descent is a widely used optimization algorithm in machine learning. It relies on updating a model’s parameters iteratively to minimize the error. Normalizing data helps gradient descent algorithms perform better by symmetrically scaling the input signals and providing a smoother and more efficient learning process.
In summary, normalizing data is essential for machine learning because it eliminates scale disparities, improves algorithm performance, facilitates feature comparison, enhances model interpretation, and enables efficient gradient descent. By taking these factors into account, data normalization ensures that machine learning models are robust, accurate, and reliable.
Benefits of data normalization
Data normalization brings several key benefits to the machine learning process. Let’s explore some of the advantages:
1. Improved accuracy: Normalizing data helps improve the accuracy of machine learning models. By bringing all variables within a specific range, models can make more precise and unbiased predictions. This is especially crucial when working with algorithms that rely on distance-based calculations, such as K-nearest neighbors or clustering techniques.
2. Robustness to outliers: Outliers, which are extreme values in the dataset, can significantly impact machine learning models. Normalization helps reduce the influence of outliers by bringing all variables to a common scale. This makes the model less sensitive to extreme values, resulting in more robust and reliable predictions.
3. Optimal algorithm performance: Normalization ensures that machine learning algorithms perform optimally. When features have similar scales, models can converge more quickly, reducing training time. Additionally, normalization facilitates the smooth flow of gradients during gradient descent, leading to faster and more efficient optimization.
4. Better comparison of feature importance: Normalizing data makes it easier to compare the importance of different features. With all variables on the same scale, it becomes straightforward to assess the relative impact of each attribute on the model’s predictions. This aids in feature selection and identifying the most influential variables in the dataset.
5. Improved model interpretability: Normalizing data enhances the interpretability of machine learning models. When variables are transformed to a common scale, the coefficients or weights assigned to each feature become more meaningful and interpretable. This allows us to understand and explain the relationship between input variables and the model’s output.
6. Efficient resource utilization: Normalization can lead to more efficient resource utilization. By reducing the range of values in the dataset, memory usage can be optimized. This is especially beneficial when working with large datasets or when deploying models in resource-constrained environments.
Overall, data normalization provides numerous benefits, including improved accuracy, robustness to outliers, optimal algorithm performance, better feature comparison, improved model interpretability, and efficient resource utilization. Considering these advantages, it is evident that normalization is a critical step in the machine learning pipeline.
The impact of non-normalized data on machine learning algorithms
The failure to normalize data can have a significant impact on the performance and reliability of machine learning algorithms. Let’s explore some of the consequences of using non-normalized data:
1. Biased results: Non-normalized data can lead to biased results in machine learning models. When features have different scales, the model may assign disproportionate importance to variables with larger values. This can skew the predictions and undermine the overall accuracy of the model.
2. Overfitting: Non-normalized data can increase the risk of overfitting. When features have varying scales, it becomes more challenging for the model to generalize patterns from the training data to unseen examples. As a result, the model may become overly specific to the training data and fail to make accurate predictions on new data.
3. Convergence issues: Machine learning algorithms that rely on optimization techniques, such as gradient descent, may face convergence issues when working with non-normalized data. Features with different scales can result in fluctuating gradients, making it harder for the algorithm to reach an optimal solution. This can lead to slow convergence or even failure to converge.
4. Difficulty in interpretation: Non-normalized data can make it challenging to interpret the model’s results. Without normalization, the weights assigned to different features may not reflect their true importance in the model. This can make it difficult to understand the impact of each variable on the model’s predictions and hinder the interpretability of the model.
5. Inefficient performance: Non-normalized data can negatively impact the performance of machine learning algorithms. When features have disparate scales, algorithms may require more iterations to converge, leading to increased computation time. This can hinder the scalability and efficiency of the models, especially when dealing with large datasets.
To mitigate these issues, it is crucial to normalize the data before feeding it into machine learning algorithms. By doing so, we ensure that data is presented in a consistent format, with similar scales and distributions. This allows algorithms to make unbiased and accurate predictions, improve interpretability, and enhance overall model performance.
In summary, non-normalized data can lead to biased results, overfitting, convergence issues, difficulties in interpretation, and inefficient performance in machine learning algorithms. Normalizing the data is essential to overcome these challenges and ensure reliable and accurate predictions.
Common normalization techniques
There are several common techniques used to normalize data in machine learning. Let’s explore some of these techniques:
1. Scaling variables to a specific range: This technique involves transforming the data so that it falls within a specific range. The most common range is between 0 and 1. To achieve this, each value is subtracted by the minimum value of the feature and then divided by the range (maximum value – minimum value). This process ensures that all variables are scaled proportionally to the defined range.
2. Standardizing variables using z-scores: Standardization, also known as z-score normalization, transforms data to have a mean of 0 and a standard deviation of 1. This technique involves subtracting the mean from each value and dividing it by the standard deviation of the feature. Standardization makes the data follow a standard Gaussian distribution, with values centered around 0. This approach is useful when the distribution of the data is important for the model’s performance.
3. Normalization by decimal scaling: Decimal scaling is a technique where each value is divided by a power of 10. The power is chosen based on the maximum absolute value in the feature. This ensures that the scaled values fall within a specific decimal range, such as -1 to 1 or -0.1 to 0.1. Decimal scaling preserves the relative ordering of the data and is particularly useful when the absolute magnitude of the feature values is essential.
4. Log transformation: Log transformation is beneficial when dealing with data that has a skewed distribution. Taking the logarithm of the values can help normalize the data and reduce the impact of extreme values. This technique is commonly used when dealing with variables such as income or population, where values span several orders of magnitude.
5. Normalization by feature engineering: Feature engineering involves creating new features by combining or transforming existing ones. This process can include techniques such as binning, where continuous variables are divided into discrete bins, or one-hot encoding, where categorical variables are converted into binary columns. These techniques can help normalize data by creating new features that follow specific distribution patterns or scale ranges.
It is essential to choose the appropriate normalization technique based on the characteristics of the data and the requirements of the machine learning algorithm. Each technique has its strengths and limitations, and the choice may vary depending on the specific problem at hand.
In summary, common data normalization techniques include scaling variables to a specific range, standardizing variables using z-scores, normalization by decimal scaling, log transformation, and normalization through feature engineering. These techniques help bring data to a standardized format, allowing machine learning models to make accurate and reliable predictions.
Scaling variables to a specific range
Scaling variables to a specific range is a common normalization technique used in machine learning. This technique ensures that all variables in a dataset are transformed to fit within a predefined range, typically between 0 and 1 or -1 and 1. Let’s explore how this technique works:
The first step in scaling variables to a specific range is to determine the minimum and maximum values for each feature. The minimum value represents the lowest value in the feature, while the maximum value represents the highest value. These values are used to establish the range within which the variables will be scaled.
To scale each variable, we subtract the minimum value of the feature from each value and then divide it by the range (maximum value – minimum value). This process ensures that all values are transformed to a proportional scale within the specified range. For example, if the minimum value is 100 and the maximum value is 500, a value of 300 would be transformed to (300 – 100) / (500 – 100) = 0.5.
The benefit of scaling variables to a specific range is that it allows for easier interpretation and comparison of feature values. Variables that have different scales can make it challenging to understand their relative importance in the model. By scaling the variables to a common range, we can directly compare and interpret the normalized values.
This technique is particularly useful when working with algorithms that rely on distance-based calculations, such as K-nearest neighbors or clustering. These algorithms can be highly sensitive to differences in scales, and scaling variables to a specific range helps mitigate this issue.
It is important to note that scaling variables to a specific range does not change the underlying distribution or shape of the data. It simply ensures that all variables have similar scales, making them easier to work with and compare.
It is worth mentioning that there are other scaling techniques, such as normalizing variables to have zero mean and unit variance using z-scores. The choice of scaling technique depends on the specific requirements of the problem and the characteristics of the data.
In summary, scaling variables to a specific range is a common normalization technique used in machine learning. By transforming variables to fit within a predefined range, we ensure that all features have similar scales, making them easier to interpret and compare. This technique is especially useful for algorithms that rely on distance-based calculations and aids in achieving accurate and reliable predictions.
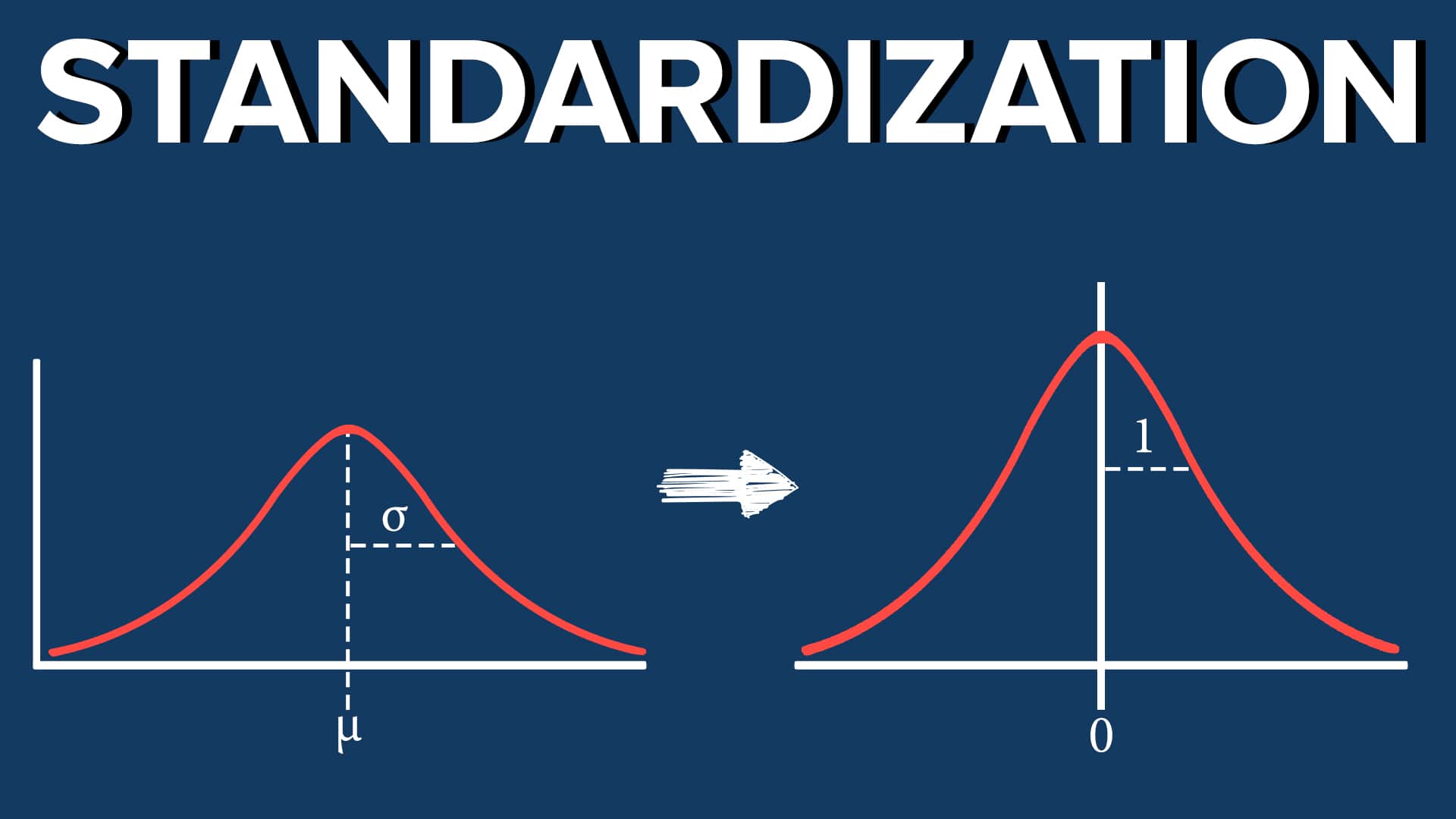
Standardizing variables using z-scores
Standardizing variables using z-scores is a widely used normalization technique in machine learning. This technique transforms data to have a mean of 0 and a standard deviation of 1. Let’s explore how this technique works:
The first step in standardizing variables using z-scores is to calculate the mean and the standard deviation of each feature. The mean represents the average value of the feature, while the standard deviation measures the dispersion of the values around the mean.
To standardize a variable, we subtract the mean of the feature from each value and then divide it by the standard deviation. This process ensures that the resulting values have a mean of 0 and a standard deviation of 1. For example, if a value is 2 and the mean of the feature is 5 with a standard deviation of 2, the standardized value would be (2 – 5) / 2 = -1.5.
The benefit of standardizing variables using z-scores is that it transforms data to follow a standard Gaussian distribution. This standardized distribution has a mean of 0 and a standard deviation of 1, which simplifies comparisons and statistical analyses.
Standardizing variables using z-scores is particularly useful when the distribution of the data is important for the model’s performance. Algorithms that rely on distance-based calculations, such as clustering or support vector machines, often perform better with standardized data.
Furthermore, standardizing variables using z-scores helps to eliminate any biases caused by differences in scales between features. When features have significantly different ranges, variables with larger scales can dominate the model’s learning process. Standardization mitigates this issue and ensures that all variables are treated equally.
It is important to note that standardization does not change the shape or distribution of the data. It simply ensures that the distribution of each variable follows a standard Gaussian distribution, with a mean of 0 and a standard deviation of 1.
Standardizing variables using z-scores is not always necessary or appropriate. For example, in some cases, maintaining the original scale and distribution of the data may be important for interpretation or domain-specific reasons. The choice of normalization technique should be based on the specific requirements of the problem and the characteristics of the data.
In summary, standardizing variables using z-scores is a common normalization technique in machine learning. It transforms data to have a mean of 0 and a standard deviation of 1, making it suitable for algorithms that rely on distance-based calculations. Standardization ensures that variables are treated equally and eliminates biases caused by differences in scales.
Handling categorical variables in normalization
When it comes to data normalization, one common challenge is how to handle categorical variables. Unlike continuous variables, categorical variables cannot be directly scaled or standardized using traditional normalization techniques. Let’s explore some approaches to handle categorical variables in normalization:
1. One-Hot Encoding: One common technique to handle categorical variables is to use one-hot encoding. This involves creating a binary column for each unique category in the variable. The binary column is set to 1 if the observation belongs to that category and 0 otherwise. One-hot encoding expands the feature space and enables the machine learning algorithm to treat each category independently. The resulting binary columns can then be normalized along with the continuous variables using appropriate normalization techniques.
2. Label Encoding: Another way to handle categorical variables is through label encoding. Label encoding assigns a numerical label to each category within a variable. This is achieved by mapping each category to a unique integer. However, it is important to note that label encoding may introduce an arbitrary order or hierarchy that doesn’t exist in the original data. Therefore, it may not be suitable for all machine learning algorithms, especially those that assume a meaningful order in the values.
3. Target Encoding: Target encoding involves replacing each category in a categorical variable with the average target value of that category. This allows the model to leverage the relationship between the categorical variable and the target variable. Target encoding can be useful when dealing with variables where the categories have varying predictive power for the outcome.
4. Binary Encoding: Binary encoding combines aspects of one-hot encoding and label encoding. It involves converting each category in a categorical variable to a binary code. This binary code represents the category as a combination of 0s and 1s. Binary encoding reduces the dimensionality of the encoded data compared to one-hot encoding while preserving some information about the categories.
When normalizing data with categorical variables, it is important to consider the specific characteristics of the dataset and the requirements of the machine learning algorithm. It is also crucial to handle categorical variables appropriately to prevent introducing biases or incorrect interpretations in the model.
In summary, handling categorical variables in normalization requires specialized techniques such as one-hot encoding, label encoding, target encoding, or binary encoding. Choosing the right approach depends on the specific dataset and the needs of the machine learning algorithm being used.
When not to normalize data
While normalization is generally beneficial for preparing data for machine learning, there are situations where it may not be necessary or appropriate. Let’s explore some scenarios when it might be best to refrain from normalizing data:
1. Domain-specific requirements: In some domains, the original scale and range of the data may hold important contextual information. For example, in finance, preserving the actual monetary values or percentages may be crucial for interpreting the results. In such cases, it is advisable to retain the original scale of the data rather than normalize it.
2. Predefined range or metric: If the data is already scaled or follows a specific range, such as a time range or a percentage, normalization may not be necessary. In these cases, applying additional normalization can distort the relationships or create unnecessary complexity in the data.
3. Algorithm requirements: Certain algorithms, such as decision trees or random forests, are not sensitive to differences in scales among variables. These algorithms make splits based on thresholds or ranks, rather than using the actual numerical values. In such cases, normalization is not crucial for the algorithm’s performance, and it may be more efficient to omit the normalization step.
4. Sparse or binary data: If the dataset consists of sparse or binary data, where the majority of the values are already 0 or 1, normalization may not bring significant benefits. In these cases, the focus may be on feature engineering techniques specific to sparse or binary data, rather than normalization.
5. Preprocessing downstream: If there are additional preprocessing steps downstream that can handle scale differences, such as robust scaling or min-max scaling as part of a feature extraction process, then normalizing the data in the initial step may be unnecessary duplication. It is important to consider the entire data pipeline when deciding whether to normalize data.
Remember that the decision of whether or not to normalize data should be based on careful consideration of the specific requirements of the problem, the characteristics of the data, and the algorithms being used. In some cases, normalization could potentially introduce biases or distort the information present in the dataset, so it is important to assess each situation individually.
In summary, there are instances when normalization may not be necessary or suitable. Factors such as domain-specific requirements, predefined ranges or metrics, algorithm insensitivity to scale, sparse or binary data, and downstream preprocessing steps should be taken into account when deciding whether or not to normalize data.
Conclusion
Data normalization is a critical step in preparing data for machine learning. It ensures that variables are on a consistent scale, enabling algorithms to make accurate predictions and improving interpretability. By bringing all features within a specific range or transforming them to follow a standard distribution, normalization eliminates biases caused by differences in scales and enhances algorithm performance.
Common techniques for data normalization include scaling variables to a specific range and standardizing variables using z-scores. Scaling variables to a specific range allows for easier interpretation and comparison of feature values, while standardization transforms data to have a mean of 0 and a standard deviation of 1, making it suitable for algorithms relying on distance-based calculations.
It is essential to handle categorical variables appropriately in the normalization process, using techniques such as one-hot encoding, label encoding, target encoding, or binary encoding. These techniques enable the inclusion of categorical information in machine learning models without introducing biases or incorrect interpretations.
However, there are cases when normalization may not be necessary or suitable. Factors such as domain-specific requirements, predefined ranges or metrics, algorithm insensitivity to scale, sparse or binary data, and downstream preprocessing steps should be considered when deciding whether or not to normalize data.
In conclusion, data normalization is a crucial step in the machine learning pipeline. It improves algorithm performance, facilitates interpretation, and ensures that all variables are treated equally. Selecting the appropriate normalization technique and assessing the need for normalization should be done in consideration of the specific characteristics of the data and the requirements of the problem at hand.