Introduction
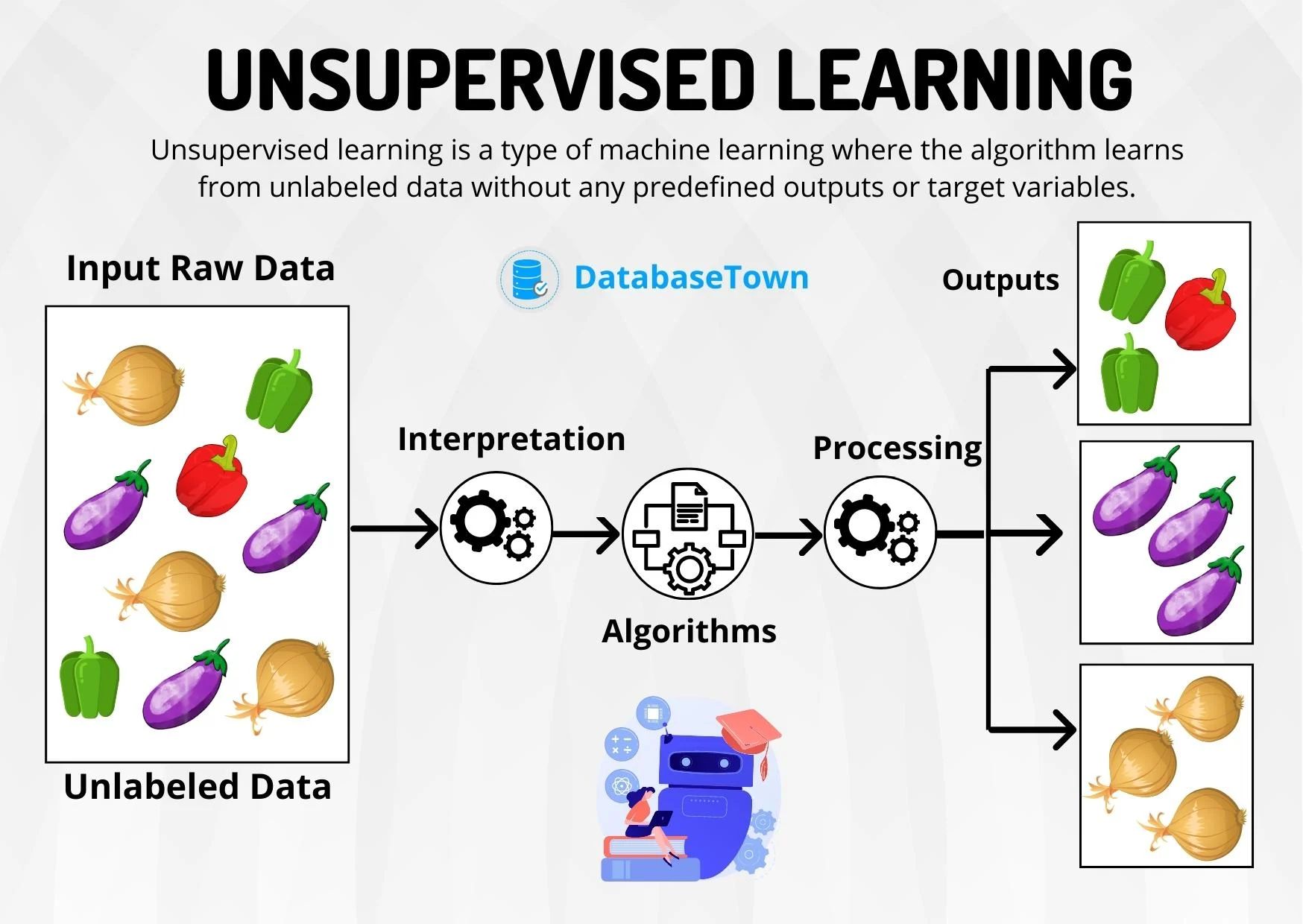
Machine learning is a powerful technique that enables computers to learn from data and make predictions or decisions without being explicitly programmed. One of the fundamental tasks in machine learning is clustering, which involves grouping similar data points together based on their characteristics. Clustering plays a crucial role in various fields such as image segmentation, customer segmentation, anomaly detection, and more.
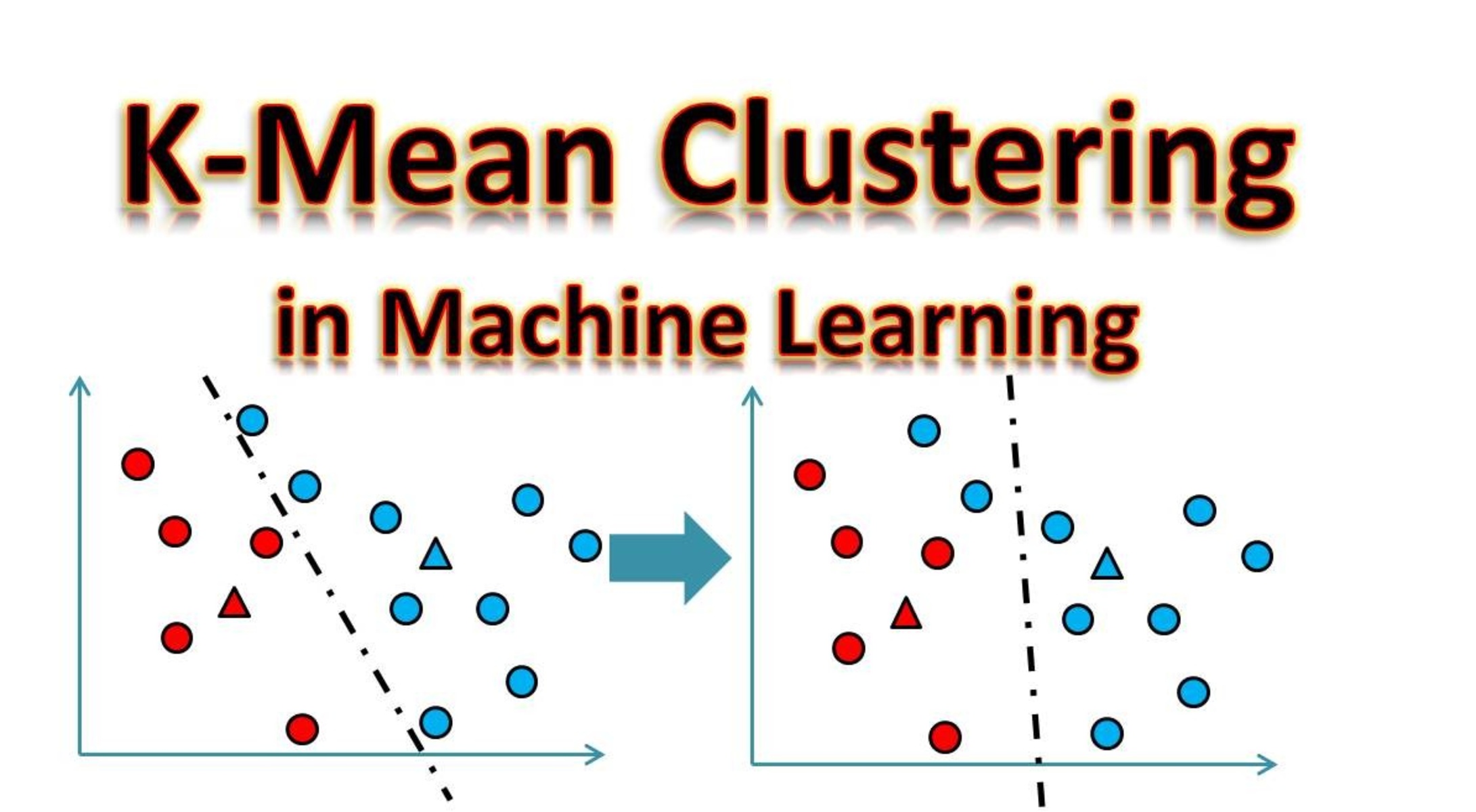
In the realm of clustering algorithms, one popular approach is K-Means clustering. K-Means clustering is an unsupervised learning algorithm that assigns data points to clusters in such a way that the points in the same cluster are similar to each other, while points in different clusters are dissimilar.
The purpose of this article is to provide a comprehensive understanding of what K-Means clustering is and how it works. We will explore the underlying concepts and steps involved in implementing K-Means clustering. Furthermore, we will discuss the advantages and limitations of this algorithm to gain insights into its utility and potential drawbacks.
By the end of this article, you will have a solid foundation in K-Means clustering and be able to apply it to your own data analysis or machine learning projects.
What is K-Means Clustering?
K-Means clustering is a popular algorithm used in unsupervised machine learning to partition data into distinct groups or clusters based on similarity. The goal of K-Means clustering is to minimize the intra-cluster variance while maximizing the inter-cluster variance.
The “K” in K-Means refers to the number of clusters that the algorithm needs to identify in the given dataset. The algorithm requires the user to specify the value of K before running the clustering process.
The basic idea behind K-Means clustering is to iteratively assign data points to clusters and update the cluster centroids until convergence is reached. The algorithm assumes that the data points can be represented by Euclidean distance in a multidimensional space.
Let’s say we have a dataset with n data points and we want to partition these points into K clusters. The algorithm starts by randomly initializing K cluster centroids. The data points are then assigned to the closest cluster centroid based on the Euclidean distance.
After the initial assignment, the algorithm recalculates the centroids of the clusters by taking the mean of all the data points assigned to each cluster. This step is repeated until the cluster assignments and centroids no longer change significantly, indicating convergence.
One of the strengths of K-Means clustering is that it is relatively fast and scalable, making it suitable for large datasets. However, it is important to note that the algorithm is sensitive to the initial placement of the cluster centroids and may converge to suboptimal solutions.
In the next section, we will delve deeper into the inner workings of the K-Means clustering algorithm and explore the steps involved in its implementation.
How does K-Means Clustering work?
Now that we have a basic understanding of what K-Means clustering is, let’s delve into the inner workings of the algorithm. K-Means clustering follows a simple yet effective iterative process to group data points into clusters.
Here are the key steps involved in the K-Means clustering process:
- Initialization: The algorithm begins by randomly selecting K data points as the initial centroids for the clusters.
- Assignment: Each data point is assigned to the closest cluster centroid based on the Euclidean distance. The centroid with the smallest distance to a data point becomes the assigned cluster for that point.
- Update Centroids: After the initial assignment, the algorithm calculates the new centroids of each cluster by taking the mean of the data points assigned to it.
- Re-Assignment: The data points are re-assigned to the updated cluster centroids based on their proximity. This step is repeated until convergence is reached.
- Convergence: Convergence is achieved when the cluster assignments and centroids no longer change significantly between iterations. This means that the algorithm has found stable cluster centroids, and the process can be terminated.
It’s important to note that the K-Means clustering algorithm does not guarantee the global optimum solution. The result obtained depends on the initial centroid placement, as well as the data distribution and shape of the clusters. Therefore, it is recommended to run the algorithm multiple times with different initializations to improve the chances of finding a better solution.
Additionally, the performance of K-Means clustering heavily relies on the choice of the value K. It is essential to evaluate the clustering results using evaluation metrics such as the Silhouette coefficient to determine the optimal number of clusters for a given dataset.
In the next section, we will discuss the implementation of K-Means clustering and the steps required to apply this algorithm to your own datasets.
How to implement K-Means Clustering
Implementing K-Means clustering involves a series of steps that can be performed using various programming languages or machine learning libraries. Here, we will outline a general approach to implementing K-Means clustering.
1. Load and preprocess the data: Start by loading the dataset that you want to cluster. Preprocess the data by normalizing or standardizing the features to ensure that they are on a similar scale.
2. Choose the number of clusters: Decide on the appropriate value for K, the number of clusters you want to create. Selecting the right number of clusters can be challenging and may require domain knowledge or utilizing evaluation metrics.
3. Initialize the cluster centroids: Randomly initialize K cluster centroids. These centroids serve as the initial representatives for each cluster.
4. Assign data points to clusters: Calculate the Euclidean distance between each data point and each cluster centroid. Assign each data point to the cluster with the nearest centroid.
5. Update the centroids: Recalculate the centroids for each cluster by taking the mean of all the data points assigned to that cluster.
6. Repeat steps 4 and 5: Iterate steps 4 and 5 until convergence is reached. Convergence occurs when the cluster assignments and centroids no longer change significantly.
7. Evaluate the clustering: Assess the quality of the clustering results using evaluation metrics such as the Silhouette coefficient or the Within-Cluster Sum of Squares (WCSS).
8. Visualize the clusters: Plot the clusters on a graph to visualize the clustering results. This can help gain insights into the structure and separation of the data.
Remember that the specific implementation details may differ depending on the programming language or library you are using. Many popular machine learning libraries, such as scikit-learn in Python or the caret package in R, provide easy-to-use implementations of the K-Means clustering algorithm.
By following these implementation steps, you can apply K-Means clustering to your own datasets and uncover meaningful patterns or groupings within the data.
Advantages of K-Means Clustering
K-Means clustering offers several advantages that make it a popular choice for data analysis and machine learning tasks. Here are some of the key advantages:
1. Simplicity: K-Means clustering is relatively simple to understand and implement. It follows a straightforward iterative process that can be easily grasped by beginners in the field of machine learning.
2. Scalability: K-Means clustering is highly scalable and can handle large datasets efficiently. The algorithm’s time complexity is generally linear with the number of data points, making it suitable for applications with a large number of observations.
3. Computational Efficiency: The simplicity of the K-Means algorithm contributes to its computational efficiency. The iterative nature of clustering allows for fast convergence, enabling real-time or near real-time analysis of data.
4. Versatility: K-Means clustering can be applied to a wide range of data types and feature spaces. It is not restricted to any particular kind of data and can handle both numeric and categorical variables with appropriate preprocessing.
5. Cluster Interpretability: The resulting clusters from K-Means clustering tend to be easily interpretable. The algorithm forms distinct clusters based on similarity, allowing for intuitive understanding and analysis of the groupings.
6. Aid in Decision-Making: K-Means clustering can assist in decision-making processes by providing insights into the underlying structure of the data. The identified clusters can help identify patterns, segment customers, detect anomalies, or support other business or research objectives.
7. Foundation for Further Analysis: K-Means clustering can serve as a foundation for more advanced data analysis techniques. It can be used as a preprocessing step or as a starting point for more complex clustering algorithms or predictive models.
While K-Means clustering offers numerous advantages, it is important to consider its limitations and potential drawbacks. In the next section, we will discuss the limitations of K-Means clustering to provide a holistic view of the algorithm.
Limitations of K-Means Clustering
While K-Means clustering has its advantages, it also has several limitations that should be taken into consideration when applying the algorithm. Understanding these limitations can help avoid potential pitfalls and ensure accurate and meaningful clustering results. Here are some of the key limitations:
1. Sensitivity to Initial Centroids: K-Means clustering’s results can vary depending on the initial placement of the cluster centroids. Different initializations might lead to different clusters or suboptimal solutions. It is recommended to run the algorithm multiple times with different initializations and select the best clustering result based on evaluation metrics.
2. Sensitive to Outliers: K-Means clustering is sensitive to outliers or noise in the data, as it seeks to minimize the total distance within clusters. Outliers can heavily influence the position and size of the centroids, potentially resulting in suboptimal clustering results. Preprocessing techniques such as outlier removal or using more robust clustering algorithms may be necessary to handle outliers effectively.
3. Assumption of Equal Cluster Sizes and Variances: K-Means clustering assumes that the clusters have an equal number of data points and similar variances. However, real-world data often does not adhere to these assumptions. If there is a significant difference in the sizes or variances of the clusters, K-Means clustering may produce biased or incorrect clustering results.
4. Shape Constraints: K-Means clustering performs well when the clusters are spherical and have similar sizes. It may struggle with complex or non-linear cluster shapes, overlapping clusters, or clusters with different densities. In such cases, other clustering algorithms like DBSCAN or Gaussian Mixture Models may be more appropriate.
5. Difficulty with High-Dimensional Data: K-Means clustering can face challenges when dealing with high-dimensional data. The curse of dimensionality can cause the Euclidean distance to lose its significance, making the algorithm less effective. Techniques such as dimensionality reduction or feature selection may be necessary to improve the clustering performance.
6. Selection of Optimal K: Choosing the optimal value for K, the number of clusters, can be subjective and challenging. An inappropriate choice of K may lead to overfitting or underfitting the data. Various evaluation metrics, such as the Silhouette coefficient, elbow method, or domain knowledge, can help in selecting a suitable value for K.
It is crucial to be aware of these limitations and evaluate the suitability of K-Means clustering for your specific dataset and objectives. Consider exploring other clustering approaches if you encounter these limitations or if your data exhibits characteristics that may not be well-suited for K-Means clustering.
Conclusion
K-Means clustering is a widely used algorithm in the field of unsupervised machine learning, offering simplicity, scalability, and versatility. It enables the partitioning of data into clusters based on similarity, aiding in various data analysis tasks, decision-making processes, and further analysis.
In this article, we explored the key aspects of K-Means clustering, from its definition to its implementation steps. We discussed the advantages of K-Means clustering, including its simplicity, scalability, and interpretability. Additionally, we highlighted some of its limitations, such as sensitivity to initial centroids, outliers, and assumptions about cluster sizes and shape constraints.
Remember that the performance of K-Means clustering depends on factors such as data preprocessing, choosing the optimal value for K, and evaluating the quality of clustering results. It’s also important to be aware of other clustering algorithms that may be better suited for certain types of data or cluster structures.
By understanding the strengths and limitations of K-Means clustering, you can effectively apply this algorithm to your own datasets and gain valuable insights. Experiment with different initializations, evaluate the clustering results, and consider utilizing other advanced techniques to improve the accuracy and robustness of your clustering solutions.
Overall, K-Means clustering serves as a valuable tool for exploratory data analysis, pattern recognition, and data-driven decision-making, offering a powerful means to uncover underlying structures and relationships in your data.