Introduction
Welcome to the fascinating world of machine learning! As you delve deeper into this field, you may come across various algorithms, techniques, and concepts that are essential for a comprehensive understanding of the subject. One such concept is the “kernel” in machine learning.
The kernel plays a crucial role in many machine learning algorithms, particularly in support vector machines (SVM), which are widely used for classification and regression tasks. Understanding what a kernel is and how it works is vital for anyone seeking to gain proficiency in machine learning.
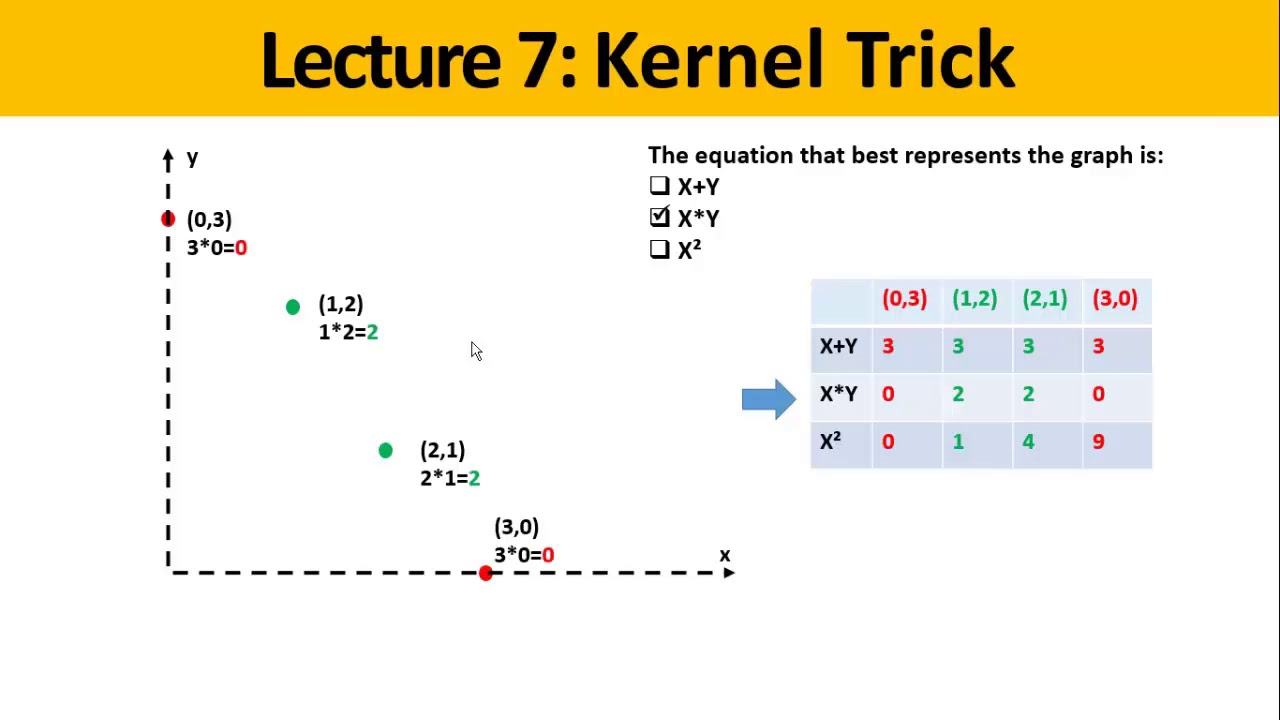
In simple terms, a kernel can be thought of as a function that quantifies the similarity between a pair of input data points. This similarity measure is crucial for various machine learning tasks, such as determining the proximity between data points, identifying patterns, and making predictions.
As we explore the world of kernels in machine learning, we will uncover the different types of kernels and their significance in the field. Additionally, we will discuss how kernels are specifically used in support vector machines, as well as explore some real-world applications of kernel-based machine learning algorithms.
By the end of this article, you will have a solid understanding of what kernels are and why they are indispensable in the realm of machine learning. So, let’s delve into the fascinating world of kernels and uncover their secrets!
Definition of Kernel
Before we dive into the different types of kernels and their applications in machine learning, let’s start by understanding what a kernel actually is.
In the context of machine learning, a kernel can be defined as a function that takes in two input data points and computes a similarity measure between them. This similarity measure quantifies the degree to which the two data points are alike or related. Essentially, a kernel helps us determine how close or similar two data points are in a given feature space.
To put it simply, a kernel acts as a transformation function that maps input data points from their original space to a higher-dimensional space, where the relationships between the data points can be more easily identified and exploited.
The concept of kernels is deeply rooted in linear algebra and functional analysis. From a mathematical standpoint, a kernel defines an inner product between two vectors in the transformed space. This inner product provides a measure of similarity or dissimilarity between the vectors and, consequently, between the original data points.
Furthermore, kernels are commonly used in machine learning algorithms to perform operations such as clustering, classification, and regression. By leveraging the power of kernels, these algorithms can effectively handle complex and non-linear relationships between input data points.
It’s important to note that the choice of kernel function depends on the specific problem at hand and the nature of the data. Different types of kernels excel in different scenarios, and selecting an appropriate kernel can greatly impact the performance of a machine learning model. Hence, understanding the properties and characteristics of different kernels is essential for effectively applying them in various machine learning tasks.
In the following sections, we will explore the different types of kernels used in machine learning and delve into their respective strengths and weaknesses. This will provide us with a deeper understanding of how kernels can be utilized to unlock the full potential of machine learning algorithms.
Types of Kernels used in Machine Learning
There are several types of kernels that are commonly used in machine learning algorithms. Each kernel has its own distinct properties and is suitable for different types of data and problem domains. Let’s explore some of the most widely used kernels:
- Linear Kernel: The linear kernel is the simplest type of kernel, and it operates in the original feature space. It calculates the dot product between two input vectors and is particularly effective when the data is linearly separable.
- Polynomial Kernel: The polynomial kernel can capture non-linear relationships between data points by computing the polynomial expansion of the dot product between input vectors. It creates complex decision boundaries and is useful in scenarios where the data exhibits polynomial patterns.
- Gaussian RBF Kernel: The Gaussian radial basis function (RBF) kernel is one of the most popular and versatile kernels. It maps the data to an infinite-dimensional space and interprets the similarity between data points as a function of the Euclidean distance between them. The RBF kernel is effective in capturing complex non-linear relationships.
- Sigmoid Kernel: The sigmoid kernel is commonly used in support vector machines (SVM) and neural networks. It utilizes the hyperbolic tangent function to transform the data and map it to a higher-dimensional space. The sigmoid kernel can handle both linear and non-linear relationships.
- Laplacian Kernel: The Laplacian kernel is similar to the Gaussian RBF kernel but uses the Laplace distribution instead of the Gaussian distribution. It assigns higher weights to data points that are closer together and is especially useful in scenarios where the data exhibits local variations.
These are just a few examples of the many types of kernels available in the field of machine learning. Each kernel has its own set of parameters that can be tuned to optimize the performance of a machine learning model. The key is to choose the appropriate kernel based on the characteristics of the data and the problem at hand.
Now that we have an understanding of the different types of kernels, let’s explore why kernels play such a crucial role in the realm of machine learning.
Importance of Kernels in Machine Learning
Kernels play a crucial role in machine learning algorithms, and their importance cannot be overstated. Here are some key reasons why kernels are vital in the field of machine learning:
1. Handling Non-linearity: Many real-world datasets exhibit complex relationships that cannot be effectively captured by linear models. Kernels enable machine learning algorithms to operate in high-dimensional feature spaces, where non-linear relationships can be more easily identified and exploited.
2. Efficient Computation: Kernels allow algorithms to compute similarity measures without explicitly mapping the data to higher-dimensional spaces. This technique, known as the “kernel trick,” avoids the computationally expensive process of explicitly calculating the transformed feature vectors. Consequently, machine learning models with kernel functions can efficiently process large datasets.
3. Flexibility and Adaptability: Kernels provide a flexible framework for handling diverse types of data. By choosing the appropriate kernel function, machine learning models can adapt to different problem domains, including image recognition, natural language processing, and financial forecasting. This adaptability makes kernels indispensable in a wide range of machine learning applications.
4. Dimensionality Reduction: Kernels can be used to transform high-dimensional data into a lower-dimensional space without losing essential information. This dimensionality reduction technique, known as kernel PCA (Principal Component Analysis), helps to mitigate the curse of dimensionality and enables more efficient data analysis.
5. Improved Performance: Kernels can significantly improve the performance of machine learning models by capturing complex patterns and relationships in the data. With the ability to model non-linear relationships, kernels enable algorithms to achieve higher accuracy and better generalization on unseen data.
6. Interpretability: In addition to enhancing prediction accuracy, kernels can also provide insights into the underlying data structures. By analyzing the learned kernel weights or support vectors, researchers and practitioners can gain a deeper understanding of the patterns and relationships within the data.
Overall, the importance of kernels in machine learning lies in their ability to handle non-linear relationships, improve computational efficiency, adapt to diverse data domains, reduce dimensionality, and enhance the overall performance of machine learning models. By leveraging the power of kernels, researchers and practitioners can unlock the potential of complex datasets and develop more robust and accurate machine learning solutions.
How Kernels are used in Support Vector Machines
Kernels and Support Vector Machines (SVM) are closely intertwined, as kernels are extensively used in SVM to solve classification and regression problems. SVM is a powerful supervised learning algorithm that finds an optimal hyperplane to separate data points of different classes. Kernels play a crucial role in SVM by enabling the algorithm to operate in higher-dimensional feature spaces and handle non-linearly separable data.
The basic idea behind SVM is to map the input data points to a higher-dimensional space where they become linearly separable. However, explicitly computing the transformed feature vectors in this higher-dimensional space can be computationally expensive, especially when dealing with large datasets. Kernels offer an elegant solution to this problem through the “kernel trick.”
The kernel trick allows SVM to efficiently compute the dot product or similarity between two data points without explicitly mapping them to the higher-dimensional space. Instead of directly calculating the transformed feature vectors, the kernel function computes the similarity measure between the data points in the original feature space. This enables SVM to operate efficiently in the higher-dimensional space and find an optimal hyperplane that maximally separates the classes.
Commonly used kernels in SVM include the linear kernel, polynomial kernel, Gaussian radial basis function (RBF) kernel, and sigmoid kernel. Each kernel has its own set of parameters that can be tuned to achieve better classification or regression performance.
For example, the linear kernel is often used when the data is linearly separable, while the RBF kernel is excellent at capturing complex non-linear relationships. The polynomial kernel is suitable for data that exhibits polynomial patterns, while the sigmoid kernel is versatile and can handle both linear and non-linear relationships.
By using kernels in SVM, we can overcome the limitations of simple linear models and unlock the potential of more complex and non-linear relationships within the data. Kernels allow SVM to handle diverse and intricate data patterns, making it a powerful tool for machine learning tasks such as image classification, text categorization, and financial prediction.
Overall, the combination of SVM and kernels provides a flexible and efficient framework for solving classification and regression problems. By leveraging the power of kernels, SVM can effectively model the relationships and patterns in the data, leading to more accurate and robust machine learning models.
Application of Kernels in Machine Learning
Kernels play a critical role in various machine learning applications, providing a powerful tool for analyzing and modeling complex data. Let’s explore some real-world applications where kernels are extensively used:
1. Image Recognition: Kernels are widely employed in image recognition tasks, where the goal is to classify images into different categories. By using kernels, machine learning models can extract relevant features from images and identify patterns that distinguish different objects or scenes. Kernels enable algorithms to handle variations in lighting, angle, and scale, making image recognition more robust and accurate.
2. Natural Language Processing: Text classification and sentiment analysis are common applications in natural language processing. Kernels can be used to extract features from textual data and classify documents into different categories. They help capture the semantic relationships between words and phrases, allowing machine learning models to make accurate predictions and identify sentiment or topic trends.
3. Speech Recognition: Kernels are employed in speech recognition to handle the complex and non-linear relationships in audio data. By transforming the audio signals into a higher-dimensional space, kernels enable algorithms to identify phonetic patterns and recognize spoken words or phrases accurately.
4. Financial Forecasting: Kernels are extensively used in financial forecasting tasks such as stock market prediction and risk analysis. By analyzing historical financial data, kernels can identify patterns and relationships that can help predict future market trends and assess investment risks. Kernels enable machine learning models to capture complex non-linear relationships between various financial indicators and make informed predictions.
5. Disease Diagnosis: Kernels play a crucial role in medical applications such as disease diagnosis and medical imaging analysis. By leveraging kernels, machine learning models can analyze complex medical data, including patient records, gene expression data, and medical images. Kernels enable algorithms to identify relevant patterns and extract features that help diagnose diseases and predict patient outcomes.
6. Fraud Detection: Kernels are employed in fraud detection systems to analyze and identify fraudulent behavior. By capturing non-linear relationships and detecting anomalies in transaction data, kernels help identify suspicious patterns that indicate potential fraud. Kernels enable machine learning models to adapt to evolving fraud patterns and detect fraudulent activities accurately.
These are just a few examples of the diverse applications of kernels in machine learning. From image recognition to fraud detection, kernels provide a versatile and powerful tool for analyzing complex data and extracting valuable insights. By leveraging kernels, machine learning models can make more accurate predictions, classify data into different categories, and uncover hidden patterns in various domains and industries.
Conclusion
In conclusion, kernels are a fundamental concept in the field of machine learning. They play a vital role in various algorithms, especially in support vector machines (SVM), by enabling non-linear classification and regression tasks. Kernels allow data to be mapped to higher-dimensional feature spaces, where complex relationships and patterns can be identified.
We explored the different types of kernels used in machine learning, including linear, polynomial, Gaussian RBF, sigmoid, and Laplacian kernels. Each kernel has its own strengths and is suitable for different types of data and problem domains. Understanding the characteristics and properties of different kernels is crucial for selecting the most appropriate one in a given scenario.
Furthermore, we discussed the importance of kernels in machine learning. Kernels help handle non-linearity, improve computational efficiency, provide flexibility and adaptability, reduce dimensionality, and enhance the overall performance of machine learning models. They enable models to capture complex patterns, make more accurate predictions, and gain insights into the underlying data structures.
Finally, we explored the application of kernels in real-world scenarios, including image recognition, natural language processing, speech recognition, financial forecasting, disease diagnosis, and fraud detection. Kernels have wide-ranging applications, providing a powerful tool for analyzing complex data and uncovering meaningful insights in various fields.
In summary, kernels are an indispensable component of machine learning algorithms. They enable algorithms to handle non-linear relationships, improve performance, and extract valuable information from data. By understanding and utilizing kernels effectively, researchers and practitioners can unlock the full potential of machine learning and develop robust and accurate models for a wide range of applications.