What Is Feature Importance In Machine Learning

Introduction

Welcome to the fascinating world of machine learning! As technology advances and data becomes more abundant, machine learning has emerged as a powerful tool for extracting insights and making predictions from large and complex datasets. One crucial aspect of building accurate and robust machine learning models is determining the importance of different features or variables in the dataset.

Feature importance refers to the process of quantifying the contribution of each feature to the predictive power of a machine learning model. By understanding which features have the most significant impact on the outcomes, we can gain valuable insights into the underlying relationships in the data and make more informed decisions.

In this article, we will delve into the concept of feature importance in machine learning and explore various methods for measuring and interpreting it. We will discuss the importance of feature selection and how it can improve the performance and interpretability of machine learning models. Additionally, we will explore the different techniques used to calculate feature importance and how they can be leveraged to gain useful insights.

Understanding feature importance can have a profound impact on various domains, including predictive analytics, risk assessment, fraud detection, and image recognition, among others. By identifying the most relevant features, we can focus our efforts on collecting and analyzing the right data, leading to more accurate and efficient models.

Throughout this article, we will explore different methods for calculating feature importance, such as permutation feature importance, feature importance from tree-based models, correlation-based feature importance, recursive feature elimination, and L1 regularization. We will also discuss the benefits and limitations of each method and uncover which approaches are best suited for different use cases.

Finally, we will delve into the interpretation and visualization of feature importance. Knowing how to effectively communicate and present feature importance results is essential for stakeholders to understand and trust the machine learning model’s outcomes. We will explore techniques for visualizing feature importance and discuss how to interpret the results to gain a deeper understanding of the underlying relationships in the data.

So, whether you are a data scientist, machine learning enthusiast, or simply curious about how machine learning models work, this article will provide you with the knowledge and practical insights to grasp the concept of feature importance and apply it in your own projects. Let’s dive in!

Definition of Feature Importance

Feature importance, in the context of machine learning, refers to the measurement of the relative influence or significance of each feature in a dataset in relation to the target variable. It helps us understand which features contribute the most valuable information to a machine learning model’s predictive power.

Features, also known as variables or attributes, are the different columns or dimensions in a dataset that provide information about each data point. They play a crucial role in training a machine learning model as they capture the patterns and relationships within the data. Feature importance allows us to identify the features that have the most impact on the model’s output or predictions.

Feature importance is especially important in scenarios where there are a large number of features in the dataset. In such cases, analyzing the significance of each feature individually can be time-consuming and challenging. By calculating feature importance, we can prioritize our analysis and focus on the most informative features, saving time and resources.

It’s worth noting that the concept of feature importance may vary depending on the type of machine learning algorithm being used. Different algorithms have different mechanisms for evaluating feature importance, and the results may not always be directly comparable across algorithms.

Feature importance can be measured in various ways. Some methods assign numeric scores to each feature, representing their relative importance or relevance. Other methods rank the features in order of importance, providing a prioritized list of the most influential features.

In summary, feature importance quantifies the contribution of each feature in a dataset to the predictive power of a machine learning model. By identifying and understanding the most influential features, we can make better decisions about feature selection, focus our analysis on the most relevant aspects of the data, and ultimately build more accurate and interpretable machine learning models.

Why is Feature Importance Important?

Feature importance plays a pivotal role in machine learning and data analysis. It provides valuable insights into the relationships and patterns within the data, contributing to the overall understanding and interpretability of the model’s predictions. Here are some key reasons why feature importance is important:

1. Identifying Relevant Features: Feature importance helps us identify the most relevant features in the dataset. By understanding which features have the most significant impact on the target variable, we can focus our analysis and decision-making efforts on the features that truly matter. This saves time, resources, and avoids potential inaccuracies caused by including irrelevant or noisy features in the model.

2. Improving Model Performance: Knowing the importance of each feature can help us build more accurate and robust machine learning models. By emphasizing the influential features and downplaying less important ones, we can achieve better predictive performance. Feature importance provides guidance for feature selection, enabling us to include only the most informative features and eliminate redundant or collinear ones.

3. Enhancing Interpretability: Feature importance aids in understanding and explaining the workings of a machine learning model. It allows us to provide meaningful insights to stakeholders and domain experts by highlighting the features that are driving the predictions or outcomes. Interpretable models are important for building trust in predictions and facilitating decision-making based on the model’s recommendations.

4. Feature Engineering: Feature importance can guide feature engineering efforts, which involve creating new features or transforming existing ones. By analyzing which features have the highest impact, we can identify potential areas for feature engineering and develop new variables that capture important patterns or interactions in the data. This iterative process can lead to more informative and powerful features, further improving model performance.

5. Insights and Understanding: Feature importance provides insights into the underlying relationships and dynamics within the data. By analyzing the top features, we can gain a deeper understanding of the factors that drive the target variable, uncover hidden patterns or correlations, and make informed decisions based on these insights. This knowledge can be leveraged not only for predictive modeling but also for gaining valuable domain-specific knowledge.

In summary, feature importance is important because it helps identify relevant features, improves model performance, enhances interpretability, guides feature engineering efforts, and provides valuable insights and understanding of the data. By harnessing the power of feature importance, we can build more accurate and meaningful machine learning models that deliver actionable insights.

Different Methods for Calculating Feature Importance

There are several methods for calculating feature importance in machine learning. Each method has its own underlying principles and assumptions, and the choice of method depends on the specific problem and dataset. Here, we discuss five popular methods for calculating feature importance:

1. Permutation Feature Importance: This method involves randomly shuffling the values of a feature and measuring the drop in model performance. The larger the drop, the more important the feature. It provides a simple and intuitive way to calculate feature importance but can be computationally expensive for large datasets.

2. Feature Importance from Tree-Based Models: Tree-based models, such as decision trees, random forests, and gradient boosting machines, provide a built-in measure of feature importance. These models analyze how often a feature is used to split the data across multiple trees and quantify its contribution to reducing impurity or error. The importance scores are then averaged or aggregated to provide an overall feature importance ranking.

3. Correlation-Based Feature Importance: This method examines the correlation between each feature and the target variable. Features with high correlation values are considered more important. However, this method assumes a linear relationship between the features and the target and may not capture non-linear patterns effectively.

4. Recursive Feature Elimination: Recursive feature elimination (RFE) works by iteratively removing the least important features from the model and assessing the impact on model performance. It provides a ranking of features based on their importance and eliminates redundant or irrelevant features. RFE can be computationally intensive but is effective for feature selection when the number of features is large.

5. L1 Regularization: L1 regularization, also known as Lasso regularization, imposes a penalty on the absolute magnitude of the feature coefficients. This encourages sparsity in the feature weights, leading to automatic feature selection. Features with non-zero coefficients are considered more important. L1 regularization is particularly useful when dealing with high-dimensional datasets.

Each method has its strengths and limitations. The choice of method depends on factors such as the nature of the data, the complexity of the problem, and the desired interpretability of the model. It is often beneficial to consider multiple methods and compare their results to gain a comprehensive understanding of feature importance.

It’s worth noting that the interpretation and comparison of feature importance values across different methods may vary. Therefore, it’s essential to analyze the results with caution and consider the specific context of the problem at hand.

By leveraging these different methods, we can effectively assess the importance of features and gain insights into the most influential aspects of our data. The selection of the appropriate method(s) for a given problem is a crucial step in building accurate and reliable machine learning models.

Permutation Feature Importance

Permutation feature importance is a simple and effective method for calculating the importance of features in a machine learning model. The key idea behind this method is to measure the drop in model performance when the values of a particular feature are randomly shuffled. The larger the drop in performance, the more important that feature is considered to be.

The process of calculating permutation feature importance involves the following steps:

1. Train the machine learning model using the original dataset and evaluate its performance (e.g., accuracy, AUC, or mean squared error).
2. Select a feature of interest.
3. Randomly shuffle the values of the selected feature while keeping the other features unchanged.
4. Re-evaluate the model performance using the randomized feature and record the drop in performance.
5. Repeat steps 3 and 4 multiple times to get an average drop in performance.

The average drop in performance indicates the importance of the feature: a larger drop implies that the feature is more important for the model’s predictions. On the other hand, a small or negligible drop suggests that the feature may have minimal impact.

Permutation feature importance is robust and can handle different types of models, including linear regression, decision trees, random forests, and neural networks. It is particularly useful when the importance of features needs to be evaluated in an agnostic manner, without making assumptions about the underlying model.

However, it is important to note that calculating permutation feature importance can be computationally expensive, especially for large datasets and complex models. Care must also be taken when dealing with highly correlated features, as permuting one feature may have an indirect impact on others.

Overall, permutation feature importance provides a valuable and interpretable way to assess the relative importance of features in a machine learning model. It helps us identify the key drivers of the model’s predictions and contributes to better feature selection, model understanding, and decision-making in various domains.

Feature Importance from Tree-Based Models

Tree-based models, such as decision trees, random forests, and gradient boosting machines, offer a built-in mechanism for calculating feature importance. These models provide a direct and intuitive measure of feature importance based on the structure and performance of the trees.

Tree-based feature importance is typically calculated by assessing how often a feature is used to make splits in the trees and how much those splits reduce impurity or error. The more frequently a feature is used and the more it reduces impurity or error, the higher its importance score.

There are different methods for calculating feature importance from tree-based models:

1. Gini Importance: Gini importance, also known as mean decrease impurity, measures the total reduction in impurity achieved by splitting on a particular feature across all the trees in a random forest. It is calculated as the weighted average of the impurity decrease for each feature over all the trees.
2. Permutation Importance: Permutation importance measures the decrease in model performance when the values of a feature are randomly shuffled. It evaluates the change in a model’s performance metric (e.g., accuracy or mean squared error) before and after shuffling the feature’s values. Features that result in a significant drop in performance have higher importance scores.
3. Information Gain or Gain Importance: For decision trees, the importance of a feature can be measured using the information gain (or gain) metric. It calculates the reduction in entropy or the impurity measure (e.g., Gini index) achieved by splitting on a particular feature.

Tree-based models offer an advantageous feature importance assessment compared to other methods because they account for feature interactions and non-linear relationships. The importance scores are generated directly from the model’s structure and provide insights into the most influential features for making predictions.

It is important to note that different tree-based models and implementations may have slight variations in how they calculate feature importance. Additionally, the importance scores may not be directly comparable across different models or algorithms. Therefore, it is recommended to consider the specific algorithm and implementation details when interpreting and comparing feature importance results.

Tree-based feature importance is widely used and has proven valuable in various applications. It aids in understanding the key drivers of predictions, supports feature selection, and guides the focus of analysis and data collection efforts.

By leveraging the built-in feature importance capabilities of tree-based models, data scientists and machine learning practitioners can gain actionable insights into the most influential features and improve the performance and interpretability of their models.

Correlation-Based Feature Importance

Correlation-based feature importance is a method that assesses the relationship between each feature and the target variable of interest. It measures the degree of correlation or association between the features and the target and uses this information to estimate feature importance.

The process of calculating correlation-based feature importance involves the following steps:

1. Compute the correlation coefficient between each feature and the target variable. The correlation coefficient indicates the strength and direction of the linear relationship between the two variables.
2. Rank the features based on their correlation coefficient values. Features with a higher absolute correlation coefficient are considered more important.
3. Optionally, apply a statistical test, such as the t-test or statistical significance test, to determine if the correlation is statistically significant.

Correlation-based feature importance is particularly useful when there is a linear relationship between the features and the target variable. It highlights the features that have the strongest linear association and suggests their relative importance for predicting the target. However, it is important to note that correlation does not imply causation, and nonlinear relationships may not be adequately captured by this method.

Another consideration is that correlation-based feature importance assumes a linear relationship between the features and the target variable. If the relationship is nonlinear or if there are complex interactions between features, other methods, such as tree-based feature importance or permutation feature importance, may provide more accurate insights.

It is also worth mentioning that correlation-based feature importance is limited to assessing direct relationships and may not capture indirect or interactive effects. For a comprehensive understanding of feature importance, it is often beneficial to combine correlation-based techniques with other methods and consider the context of the specific problem.

Despite these limitations, correlation-based feature importance provides a straightforward and interpretable way to identify features that have a strong linear relationship with the target variable. It can guide feature selection, help prioritize certain variables in a model, and provide initial insights into the influence of features on the target variable. However, it is important to consider the underlying assumptions and limitations of this method when interpreting the results.

Recursive Feature Elimination

Recursive Feature Elimination (RFE) is a versatile method for feature selection that aims to identify the most important features by iteratively eliminating the least relevant ones. RFE is particularly useful when dealing with datasets that have a large number of features or when the goal is to improve model performance and interpretability by selecting a subset of the most informative features.

The process of Recursive Feature Elimination involves the following steps:

1. Train a machine learning model on the entire set of features.
2. Rank the features based on their importance scores according to the chosen model’s built-in feature importance measure.
3. Remove the least important feature(s) from the dataset.
4. Re-train the model using the reduced feature set.
5. Repeat steps 2-4 until a desired number of features or a specific performance threshold is reached.

RFE eliminates features based on their importance scores, which are typically calculated using a model-specific metric such as Gini importance or coefficient magnitudes. The iterative elimination process helps identify the optimal subset of features that maximizes performance while minimizing redundancy or noise.

One advantage of RFE is that it takes into account the interactions and dependencies between features. By considering feature importance in relation to the current model state, RFE progressively selects the most informative features while accounting for their collective impact.

However, it is important to note that RFE can be computationally intensive, especially for datasets with a large number of features. Additionally, the performance of RFE may vary based on the choice of the model and the metric used to calculate feature importance. It is crucial to carefully select the appropriate model and metric that aligns with the specific problem at hand.

RFE provides a systematic and automated approach to feature selection, eliminating the need for manual feature inspection and ranking. It helps simplify models, reduce dimensionality, enhance model interpretability, and potentially improve prediction accuracy by focusing on the most relevant features.

It is worth noting that RFE is not the only method for feature selection, and its effectiveness may depend on the specific dataset and problem domain. It is often beneficial to compare RFE’s results with other feature selection methods and consider the trade-offs between model complexity, interpretability, and performance.

Overall, Recursive Feature Elimination is a valuable tool in the data scientist’s arsenal, enabling the selection of the most important features while improving the efficiency and interpretability of machine learning models.

L1 Regularization

L1 regularization, also known as Lasso regularization, is a technique used to select relevant features by encouraging the sparsity of feature weights in a machine learning model. It achieves this by adding a penalty term to the loss function that pushes the model to reduce the absolute magnitude of the feature coefficients.

The process of applying L1 regularization involves the following steps:

1. Train a machine learning model, such as linear regression or logistic regression, without any regularization.
2. Add an L1 regularization term to the loss function, which penalizes the sum of the absolute values of the feature coefficients.
3. Tune the regularization parameter, typically denoted as lambda or alpha, to control the amount of regularization applied. Higher values of lambda result in more aggressive feature selection.
4. Fit the model with the L1 regularization term and obtain the feature coefficients.
5. Identify features with non-zero coefficients as the most important features.

L1 regularization promotes feature selection by driving some of the feature coefficients to zero, effectively removing those features from the model. The remaining non-zero coefficient features are selected as the most important predictors.

One advantage of L1 regularization is its ability to automatically perform feature selection and eliminate irrelevant or redundant features. It can be particularly useful in high-dimensional datasets where the number of features exceeds the number of observations. By shrinking some feature coefficients to zero, L1 regularization simplifies the model, enhances interpretability, and reduces overfitting.

Another benefit of L1 regularization is its flexibility to be applied to various machine learning models, including linear and logistic regression, as well as their regularized counterparts such as Lasso regression and Elastic Net.

However, it is important to note that L1 regularization assumes that the relationship between the predictors and the target variable is linear. If the relationship is non-linear, other methods like tree-based feature importance or permutation feature importance may yield more accurate results.

L1 regularization strikes a balance between feature importance and model complexity by automatically selecting relevant features while discarding irrelevant ones. By harnessing its power, data scientists can streamline their models, reduce overfitting, and gain insights into the most important predictors for their machine learning task.

Comparing Different Methods for Feature Importance

When it comes to calculating feature importance in machine learning, there are several methods available, each with its own strengths and limitations. Comparing these methods allows us to gain a deeper understanding of the data and select the most appropriate technique for a given problem. Let’s explore some key considerations when comparing different methods:

Methodology: The methods for calculating feature importance vary in their underlying principles and assumptions. Some methods, like permutation feature importance, are model-agnostic and can be applied to any model type. Others, such as tree-based feature importance, leverage the internal workings of specific models. It’s important to consider the method’s compatibility with the model and the problem at hand.

Interpretability: Different methods can provide varying levels of interpretability. For instance, correlation-based feature importance offers straightforward insights into the linear relationship between features and the target variable. On the other hand, methods like tree-based feature importance can unveil complex interactions and non-linear relationships. The level of interpretability required for a specific use case influences the choice of method.

Data Characteristics: The characteristics of the dataset, including its size, dimensionality, and type of features, can impact the choice of feature importance method. For example, permutation feature importance can be computationally expensive for large datasets, while correlation-based methods assume linearity between features and the target. It’s important to assess how well the method aligns with the data’s characteristics.

Robustness and Consistency: Robustness refers to the method’s ability to produce consistent and reliable results. Different feature importance methods may provide different rankings or importance scores for the same dataset. Evaluating the robustness of each method through multiple runs or cross-validation can help ensure the reliability of the results.

Complementarity: Feature importance methods are not mutually exclusive. In fact, they can be complementary, offering different perspectives on the importance of features. It is often beneficial to compare and contrast the results from multiple methods to gain a more comprehensive understanding of the data and uncover nuanced insights.

Ultimately, the choice of feature importance method depends on the specific data, problem, and desired outcomes. It is often recommended to experiment with multiple methods, evaluate their results, and consider the trade-offs between interpretability, computational complexity, and the specific requirements of the problem at hand.

By comparing different methods for feature importance, we can make more informed decisions, gain a deeper understanding of the data, and select the most appropriate approach to extract valuable insights from the features in our machine learning models.

Interpretation and Visualization of Feature Importance

Interpreting and visualizing feature importance is crucial for effectively communicating and understanding the impact of different features in a machine learning model. It helps stakeholders gain insights into the underlying relationships, make informed decisions, and build trust in the model’s outcomes. Here are some considerations for interpreting and visualizing feature importance:

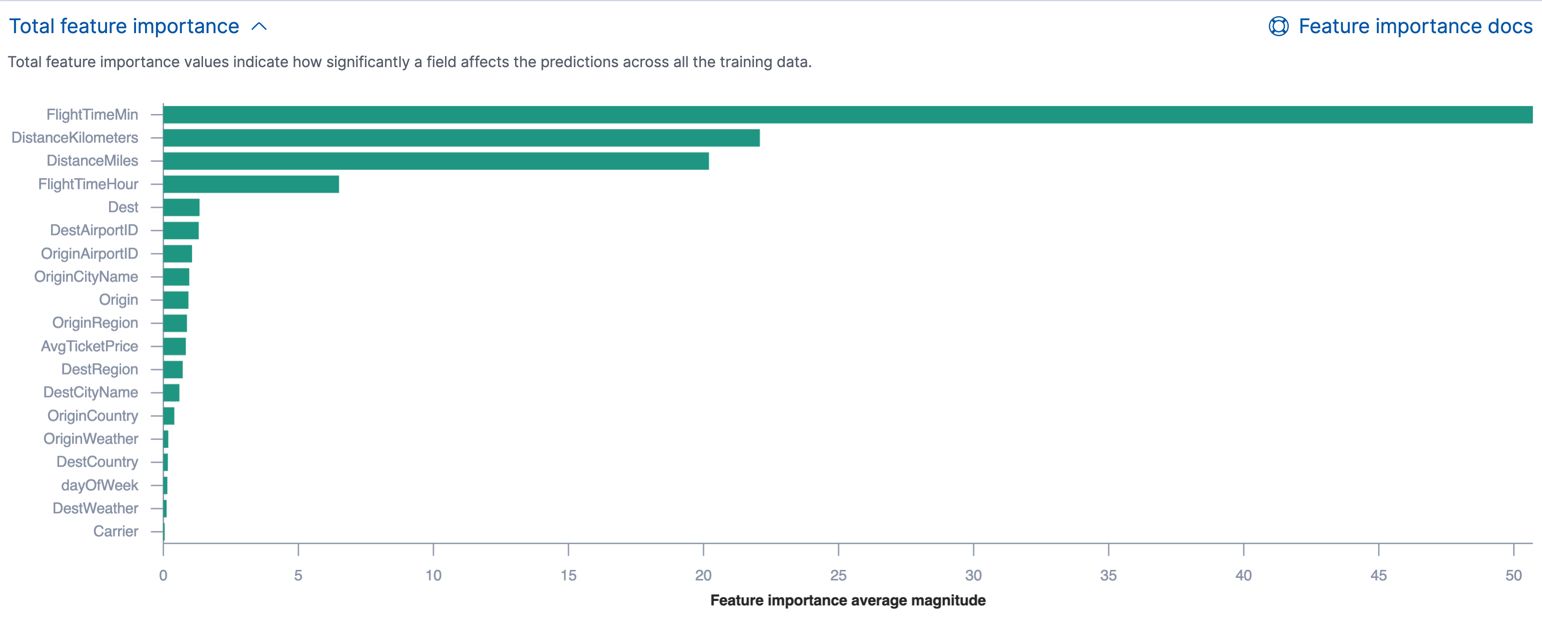
Ranking and Importance Scores: One common approach is to rank the features based on their importance scores. This provides a straightforward way to identify the most influential features. The ranking can be presented in a tabular format, with the feature names and their corresponding scores, making it easy to view and compare their relative importance.

Visualizing Importance Scores: Visualizing feature importance scores can enhance their interpretation and make the insights more accessible. Bar charts, for example, can be used to display the importance scores for each feature, allowing for quick visual comparison. Heatmaps or color-coded scatter plots can also be used to highlight the relationships between features and their importance.

Feature Contributions: Beyond just ranking features, it can be valuable to understand how each feature contributes to the model’s predictions. For tree-based models, visualizing individual decision paths and the splits made by important features can provide insights into how they influence the final outcome.

Feature Interaction: In some cases, the importance of a single feature may not tell the whole story. It can be useful to assess the interaction effects between features. By visualizing feature interactions, such as scatter plots, heatmaps, or network diagrams, we can uncover synergistic or antagonistic relationships that contribute to the overall prediction.

Domain-Specific Interpretation: Interpreting feature importance also requires domain-specific knowledge and context. Understanding the meaning and implications of a feature’s importance within the domain can provide deeper insights and enable more informed decisions.

Considering Feature Correlations: Feature importance scores can sometimes be influenced or biased by highly correlated features. Visualizing correlation matrices or pairwise scatter plots can help identify such relationships and ensure the interpretation of feature importance is accurate.

Overall, interpreting and visualizing feature importance goes beyond raw numbers. It involves conveying the meaning, influence, and relationships of features in a clear and meaningful way. By using appropriate visualization techniques and considering domain knowledge, we can effectively communicate the importance of features and provide valuable insights to stakeholders.

Conclusion

Feature importance is a crucial aspect of machine learning and data analysis. It enables us to understand the relative importance and impact of different features on the outcomes of a model. By assessing feature importance, we can make better decisions in data collection, feature selection, and modeling processes.

In this article, we explored various methods for calculating feature importance, including permutation feature importance, feature importance from tree-based models, correlation-based feature importance, recursive feature elimination, and L1 regularization. Each method offers unique insights and considerations, catering to different types of data and problem domains.

Interpretation and visualization of feature importance are essential for effectively communicating the importance of features to stakeholders. Ranking features, visualizing importance scores, understanding feature contributions and interactions, and considering domain-specific interpretations all contribute to a better understanding of the underlying relationships and help build trust in the model’s predictions.

It is important to note that feature importance is not a one-size-fits-all concept. The choice of method and interpretation may depend on the specific problem, data, and desired outcomes. It is often beneficial to compare and contrast the results from different methods, considering their strengths and limitations, to gain comprehensive insights.

In conclusion, by leveraging the power of feature importance, we can enhance the performance, interpretability, and efficiency of our machine learning models. By choosing appropriate methods, interpreting the results effectively, and visualizing the importance of features, we can uncover valuable insights, make informed decisions, and drive impactful outcomes in various domains.