Introduction
Machine learning algorithms have emerged as powerful tools for extracting valuable insights from data. These algorithms are capable of learning patterns, making predictions, and aiding in decision-making processes. However, the performance of a machine learning model heavily relies on its configuration and parameter settings. This is where tuning comes into play.
Tuning in machine learning refers to the process of selecting the optimal set of hyperparameters for a given algorithm. Hyperparameters are parameters that are not learned from the data but rather set by the user prior to the training process. These include parameters such as learning rates, regularization terms, kernel types, and many others. Properly tuning these hyperparameters can significantly impact the performance and accuracy of the model.
Tuning is necessary because different datasets and problems require different hyperparameter configurations to achieve optimal results. It is not always possible to choose the best hyperparameters manually, as the search space can be large and complex. Therefore, various tuning methods are developed to automate this process and find the best hyperparameter values.
In this article, we will explore the concept of tuning in machine learning, the need for tuning, and the different methods used for finding optimal hyperparameters. We will also provide some best practices to guide you in the tuning process.
Tuning is an essential step in the machine learning pipeline as it allows us to maximize the model’s performance and generalizability. By finding the optimal hyperparameters, we can ensure that the model is not underfitting or overfitting the data. This leads to improved accuracy, robustness, and reliability of the trained model.
In the following sections, we will delve into the various tuning methods available, ranging from grid search and random search to more advanced techniques like Bayesian optimization, simulated annealing, and genetic algorithms. These methods provide automated ways to explore the hyperparameter space and find the best configuration for our model.
It is worth noting that tuning is a time-consuming process that requires computational resources. However, it is a crucial step that can significantly affect the performance of your machine learning model. By investing time and effort into tuning, you can unlock the full potential of your algorithms and achieve better results.
Now that we understand the importance and need for tuning in machine learning, let’s dive deeper into the different tuning methods available and how they can help us find the best hyperparameter values for our models.
What Is Tuning in Machine Learning?
Tuning in machine learning refers to the process of optimizing the performance of a machine learning model by selecting the best values for its hyperparameters. Hyperparameters are parameters that are set by the user, rather than learned from the data, and they control the behavior of the algorithm during training. Examples of hyperparameters include learning rates, regularization parameters, number of hidden layers in a neural network, and kernel types in support vector machines.
The performance of a machine learning model is greatly influenced by its hyperparameter settings. Choosing the right values for these parameters is crucial to achieve good accuracy and generalization on new data. However, determining the optimal hyperparameter values is not a straightforward task. It requires an understanding of the algorithm, the problem at hand, and careful experimentation.
Tuning is necessary because there is no one-size-fits-all set of hyperparameters that works well for all datasets and problems. Different datasets and problem domains have different characteristics and complexities, making it impossible to have a universal set of hyperparameters that guarantees the best performance. By tuning the hyperparameters, we aim to find the best configuration that maximizes the model’s performance on a specific problem.
There are various methods available for tuning hyperparameters, ranging from manual tuning to automated techniques. Manual tuning involves manually adjusting the hyperparameter values based on intuition, domain knowledge, and trial and error. While this approach can sometimes yield good results, it is highly time-consuming and not scalable to large search spaces.
Automated tuning methods, on the other hand, provide a more systematic and efficient way of exploring the hyperparameter space. These methods automate the process of searching for the best hyperparameter values by evaluating different combinations and selecting the ones that yield the best results.
One commonly used automated tuning method is grid search. Grid search involves specifying a set of possible values for each hyperparameter and exhaustively searching through all possible combinations. It is a brute-force approach that can be computationally expensive, especially for large hyperparameter spaces.
Random search is another popular tuning method that offers a more efficient alternative to grid search. Instead of exploring all possible combinations, random search samples random combinations of hyperparameters over a given search space. This approach is more effective at finding good hyperparameters and requires fewer evaluations than grid search.
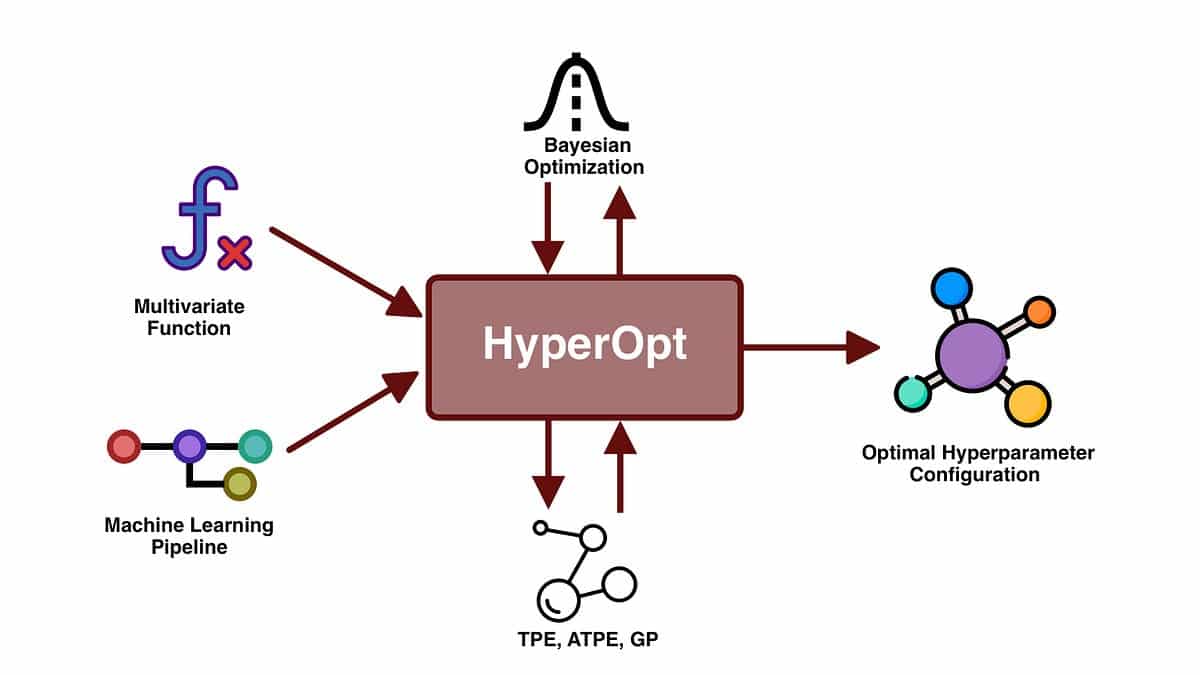
Bayesian optimization is a more advanced tuning method that uses probabilistic models to guide the search in the hyperparameter space. By leveraging the information gained from previous evaluations, Bayesian optimization can intelligently search for promising regions and quickly converge to the optimal hyperparameter values.
Other methods, such as simulated annealing and genetic algorithms, borrow concepts from optimization and evolution to find the best hyperparameters. These methods simulate the annealing of a physical system or the evolutionary process to iteratively search for optimal solutions in the hyperparameter space.
Recently, automated machine learning (AutoML) frameworks have gained popularity. These frameworks aim to automate the entire machine learning pipeline, including data preprocessing, feature selection, model selection, and hyperparameter tuning. AutoML platforms provide an end-to-end solution for building machine learning models without the need for manual intervention.
In summary, tuning in machine learning is the process of finding the optimal values for hyperparameters to maximize the performance and generalization of a model. It plays a crucial role in achieving good accuracy and robustness. Manual and automated tuning methods, such as grid search, random search, Bayesian optimization, simulated annealing, and genetic algorithms, offer different approaches to explore the hyperparameter space and find the best configuration for a given problem.
The Need for Tuning
Tuning is a critical step in machine learning because it allows us to optimize the performance of our models to achieve better accuracy and generalization. Here are some reasons why tuning is necessary:
1. Performance Optimization: Different hyperparameter settings can have a significant impact on the performance of a machine learning model. By tuning these hyperparameters, we can fine-tune the model to achieve the best possible performance. This is particularly important when dealing with complex datasets or when working on tasks that require high accuracy, such as image recognition or fraud detection.
2. Overfitting and Underfitting Prevention: Overfitting and underfitting are common problems in machine learning. Overfitting occurs when a model becomes too complex and fits the training data too closely, resulting in poor performance on new, unseen data. Underfitting, on the other hand, happens when a model is too simple and fails to capture the underlying patterns in the data. Tuning can help prevent these issues by finding the right balance between model complexity and performance.
3. Dataset Variability: Datasets can vary significantly in terms of size, complexity, and distribution. What works well for one dataset may not work well for another. Tuning allows us to adapt the model to the specific characteristics of the dataset and account for any inherent biases or patterns that may exist. By fine-tuning the hyperparameters, we can make the model more robust and improve its performance on diverse datasets.
4. Domain Knowledge and Constraints: In many real-world applications, there are domain-specific knowledge and constraints that need to be considered. For example, in healthcare, there may be regulations or ethical considerations that impact the selection of hyperparameters. Tuning allows us to incorporate domain knowledge and constraints into the model by customizing the hyperparameters accordingly.
5. Generalization: One of the primary goals of machine learning is to build models that can generalize well to unseen data. Tuning helps improve the generalization capability of models by finding the hyperparameter values that lead to the best performance on both the training and validation data. This ensures that the model is not overly specialized to the training data and can make accurate predictions in real-world scenarios.
6. Model Interpretability: Some hyperparameters in machine learning algorithms can affect the interpretability of the model. For example, in decision trees, the maximum depth parameter controls the complexity of the tree and the interpretability of the resulting rules. By tuning these hyperparameters, we can strike a balance between model performance and interpretability, depending on the specific requirements of the problem.
Tuning is not a one-time process and may need to be performed iteratively. As new data becomes available or the problem evolves, it may be necessary to revisit the hyperparameter settings and fine-tune the model accordingly. By continuously refining the hyperparameters, we can ensure that the model remains up-to-date and continues to deliver optimal performance.
In summary, the need for tuning in machine learning arises from the desire to optimize model performance, prevent overfitting and underfitting, handle dataset variability, incorporate domain knowledge and constraints, improve generalization, and balance model interpretability. By carefully tuning the hyperparameters, we can unlock the full potential of our machine learning models and achieve better results on a wide range of problems.
Hyperparameters and Tuning
In machine learning, hyperparameters are parameters that are set before the learning process begins. Unlike model parameters, which are learned from the data, hyperparameters control the behavior of the algorithm during training and affect the performance and generalization of the model. Tuning involves selecting the optimal values for these hyperparameters to achieve the best possible results.
Hyperparameters can vary depending on the algorithm and the specific problem. For example, in a neural network, hyperparameters may include the learning rate, the number of hidden layers, the number of neurons in each layer, the activation functions, and the regularization strength. In a support vector machine, hyperparameters may include the kernel type, the regularization parameter, and the degree of the polynomial kernel.
Each hyperparameter has a range of possible values that can be assigned to it. The challenge lies in finding the best combination of values that maximizes the model’s performance. This is where tuning comes into play. By systematically exploring different combinations of hyperparameters and evaluating their impact on the model’s performance, we can determine the optimal set of hyperparameter values.
Tuning hyperparameters is a crucial step in machine learning because it allows us to avoid underfitting and overfitting. Underfitting occurs when the model is too simple and fails to capture the underlying patterns in the data. As a result, the model’s performance is poor both on the training data and new, unseen data. Overfitting, on the other hand, happens when the model becomes too complex and fits the training data too closely. As a result, the model performs well on the training data but fails to generalize to new data.
Tuning hyperparameters can also help optimize the performance of the model. By selecting the best hyperparameter values, we can improve accuracy, reduce error rates, and enhance the model’s ability to make accurate predictions. Moreover, tuning can help fine-tune the trade-off between model complexity and performance. For instance, in a decision tree, tuning the maximum depth hyperparameter can determine the level of complexity and the interpretability of the resulting tree.
There are different approaches to tuning hyperparameters, both manual and automated. Manual tuning involves adjusting the values through trial and error or domain knowledge. It requires expertise and can be time-consuming, especially in the case of complex models with a large number of hyperparameters. Automated tuning methods, on the other hand, provide a systematic way to explore the hyperparameter space and find optimal values.
Popular automated tuning methods include grid search, random search, Bayesian optimization, simulated annealing, and genetic algorithms. Grid search exhaustively evaluates all possible combinations of hyperparameters, making it comprehensive but computationally expensive. Random search randomly samples combinations of hyperparameters, providing a more efficient alternative to grid search. Bayesian optimization employs probabilistic models to guide the search process, while simulated annealing and genetic algorithms simulate optimization and evolution to find optimal values.
In summary, hyperparameters are parameters that control the behavior of the machine learning algorithm. Tuning, the process of selecting optimal values for these hyperparameters, plays a critical role in avoiding underfitting and overfitting, optimizing model performance, and fine-tuning the trade-off between complexity and interpretability. Manual and automated tuning methods offer ways to explore the hyperparameter space and find the best configuration for a given problem.
Types of Tuning Methods
When it comes to tuning hyperparameters in machine learning, there are various methods available to automate and streamline the process. These methods differ in their strategies and algorithms for exploring the hyperparameter space and finding the optimal set of values. Let’s explore some of the common types of tuning methods:
1. Grid Search: Grid search is a simple and systematic approach where a predefined set of values is specified for each hyperparameter. The algorithm exhaustively evaluates all possible combinations of these values to find the best set of hyperparameters. While grid search is comprehensive, it can be computationally expensive, especially when dealing with a large number of hyperparameters or a wide range of values.
2. Random Search: Random search is a more efficient alternative to grid search. Instead of exploring all combinations, random search samples a predefined number of random combinations from the hyperparameter space. By selecting combinations randomly, the search process covers a wider range of values and has the potential to find better solutions with fewer evaluations. Random search is particularly useful when the hyperparameter space is large or the relationship between hyperparameters is unknown.
3. Bayesian Optimization: Bayesian optimization is a sophisticated method that uses probabilistic models to guide the search for optimal hyperparameters. By leveraging past evaluations, Bayesian optimization builds a probabilistic model of the objective function and uses it to make informed decisions on which set of hyperparameters to evaluate next. This approach allows for efficient exploration of the hyperparameter space while simultaneously exploiting promising regions. Bayesian optimization is especially useful when the evaluation of a hyperparameter configuration is expensive or time-consuming.
4. Simulated Annealing: Simulated annealing is a heuristic optimization algorithm inspired by the physical annealing process. It starts with an initial set of hyperparameters and iteratively explores the neighboring search space by randomly perturbing the current configuration. The algorithm accepts worse solutions early in the process but gradually becomes more selective as it progresses, emulating the cooling of a metallic object during annealing. Simulated annealing can be useful in exploring complex and rugged hyperparameter landscapes and escaping from local optima.
5. Genetic Algorithms: Genetic algorithms are a class of evolutionary algorithms that are inspired by the process of natural selection and genetic variation. In the context of hyperparameter tuning, genetic algorithms start with an initial population of hyperparameter configurations and iteratively apply genetic operators such as mutation, crossover, and selection to generate new offspring. This allows the algorithm to explore different combinations of hyperparameters and converge towards an optimal solution. Genetic algorithms are particularly effective when dealing with large hyperparameter spaces or when there may be interactions between different hyperparameters.
6. Automated Machine Learning: Automated Machine Learning (AutoML) platforms offer a comprehensive solution for the entire machine learning pipeline, including hyperparameter tuning. These platforms streamline the process by automatically selecting and optimizing the hyperparameters for different machine learning models. AutoML employs a combination of strategies, including grid search, random search, and Bayesian optimization, to find the best hyperparameter configuration. The advantage of AutoML is that it eliminates the need for manual intervention and is well-suited for users who lack expertise in hyperparameter tuning.
Each of these tuning methods has its strengths and weaknesses. The choice of which method to use depends on factors such as the size of the hyperparameter space, the complexity of the problem, the computational resources available, and the trade-off between accuracy and runtime. It is essential to experiment with different methods and find the one that best suits your specific needs.
In summary, there are several types of tuning methods available in machine learning. These include grid search, random search, Bayesian optimization, simulated annealing, genetic algorithms, and automated machine learning. Each method offers a different strategy for exploring the hyperparameter space and finding the optimal set of values. By leveraging these tuning methods, we can enhance the performance and generalization of our machine learning models.
Grid Search
In the realm of hyperparameter tuning, grid search is a popular and straightforward method that systematically explores the entire search space of hyperparameters to find the optimal combination. It is often the first method tried due to its simplicity and comprehensiveness.
Grid search involves specifying a set of possible values for each hyperparameter of interest. The algorithm then exhaustively evaluates all possible combinations of these values. It performs a systematic search over a predetermined grid of hyperparameter values, hence the name “grid search.”
For example, let’s say we have a machine learning model with two hyperparameters: learning rate and number of hidden units. We can specify a grid of potential values for each hyperparameter. Suppose we choose learning rates of 0.01, 0.1, and 0.001, and hidden unit values of 50, 100, and 200. Grid search will then evaluate the model’s performance using all nine possible combinations of these values.
Grid search is beneficial because it offers a comprehensive search of the hyperparameter space. It ensures that every combination is considered and evaluated, providing a complete overview of the model’s performance across all hyperparameter settings. This is particularly useful when the relationship between hyperparameters and model performance is not well understood.
However, one drawback of grid search is its computational cost. As the number of hyperparameters and their potential values increase, the total number of combinations grows exponentially. This can quickly become computationally prohibitive, especially when working with large datasets or complex models.
To mitigate the computational burden, it is common to combine grid search with techniques such as cross-validation. By using techniques such as k-fold cross-validation, grid search can estimate the performance of each hyperparameter combination more accurately using multiple train-test splits. This not only provides better performance estimates but also helps prevent overfitting on the training data.
To implement grid search, various machine learning libraries and frameworks provide utilities that simplify the process. These utilities handle the repetitive evaluation of different hyperparameter configurations and allow users to specify the search space and evaluation metric easily.
In summary, grid search is a systematic method for tuning hyperparameters by evaluating all possible combinations. It offers an exhaustive search of the hyperparameter space and provides valuable insights into the performance of a model across various configurations. Although computationally expensive, grid search can be combined with cross-validation to improve performance estimation and prevent overfitting.
Random Search
Random search is a popular method for hyperparameter tuning in machine learning that offers a more efficient alternative to grid search. Instead of exhaustively evaluating all possible combinations of hyperparameter values, random search randomly samples different combinations from the search space. This random sampling allows for a broader exploration of the hyperparameter space and has the potential to find better solutions with fewer evaluations.
The process of random search involves defining a search space for each hyperparameter, specifying the distribution or range of values from which to sample. The algorithm then randomly selects hyperparameter values from these distributions or ranges and evaluates the model’s performance using these random configurations.
Compared to grid search, random search is advantageous in scenarios where the relationship between hyperparameters and model performance is not well understood or when the search space is large and complex. It can effectively search through a wider range of hyperparameter values, potentially discovering better combinations that grid search might miss.
Another key advantage of random search is its computational efficiency. Randomly sampling combinations of hyperparameters reduces the number of evaluations required compared to grid search, especially when the search space is large or when some hyperparameters have little impact on the model’s performance. This efficiency allows random search to handle complex problems and larger datasets more effectively.
One consideration when using random search is the choice of the sampling distribution or range for each hyperparameter. The search space should be carefully determined, taking into account any prior knowledge or assumptions about the hyperparameters. For some hyperparameters, such as learning rates, it is common to use a logarithmic scale to cover a wide range of values more evenly.
Random search can also be combined with techniques such as cross-validation to estimate the performance of each randomly evaluated hyperparameter configuration more accurately. By using k-fold cross-validation, the model’s performance is assessed over multiple train-test splits, providing a more reliable performance estimate.
Many machine learning libraries and frameworks provide built-in functions and utilities for random search. These utilities enable easy specification of the search space and automate the random sampling and evaluation of hyperparameter configurations. This makes the implementation of random search more efficient and user-friendly.
In summary, random search is a technique for hyperparameter tuning that randomly samples hyperparameter configurations from a defined search space. Compared to grid search, random search offers computational efficiency and the ability to explore a wider range of hyperparameter values. It is particularly useful for problems with a complex search space or when the relationship between hyperparameters and model performance is unclear. By combining random search with techniques like cross-validation, it is possible to efficiently and effectively tune hyperparameters and improve the performance of machine learning models.
Bayesian Optimization
Bayesian optimization is a powerful method for hyperparameter tuning in machine learning that employs probabilistic models to guide the search process. It combines ideas from probability theory and optimization to intelligently search the hyperparameter space and find the optimal set of values for a given objective.
The key idea behind Bayesian optimization is to construct a probabilistic model known as a surrogate model or surrogate function that approximates the true objective function, which maps hyperparameter configurations to their corresponding performance. This surrogate model is updated at each iteration of the optimization process based on the evaluated hyperparameter configurations. The surrogate model provides a probabilistic estimate of the objective function, allowing Bayesian optimization to make informed decisions about which hyperparameter configurations to evaluate next.
Bayesian optimization uses an acquisition function to balance the exploration-exploitation trade-off. The acquisition function determines the next hyperparameter configuration to evaluate by considering both the surrogate model’s uncertainty and the current knowledge of the objective function. Popular acquisition functions include Expected Improvement (EI), Probability of Improvement (PI), and Upper Confidence Bound (UCB).
One of the advantages of Bayesian optimization is its ability to efficiently explore the hyperparameter space while also exploiting promising regions. The surrogate model continuously updates and learns from the evaluated hyperparameter configurations, allowing Bayesian optimization to focus its search on the most relevant parts of the search space. This adaptive nature makes it particularly effective when there are limited evaluations available or when the cost of evaluating a configuration is high.
Bayesian optimization is especially valuable when evaluating hyperparameter configurations is computationally expensive or time-consuming, as it minimizes the number of evaluations required to find the optimal set of hyperparameters. It also provides a principled way to handle noise in the objective function and facilitates the acquisition of a robust and reliable set of hyperparameter values.
Implementing Bayesian optimization typically involves specifying the search space and an acquisition function, as well as choosing a surrogate model, such as Gaussian Processes or Random Forests, to approximate the objective function. Various machine learning libraries and frameworks provide tools and utilities to simplify the implementation of Bayesian optimization.
It is worth noting that Bayesian optimization is not without certain limitations. The choice of surrogate model and acquisition function can have an impact on its performance, and finding the right combination for a specific problem may require some experimentation. Additionally, Bayesian optimization may struggle with high-dimensional search spaces due to the curse of dimensionality. However, there are techniques, such as dimensionality reduction and sequential model-based optimization, that can help address this issue.
Overall, Bayesian optimization is a versatile and powerful method for hyperparameter tuning. By leveraging probabilistic models and intelligent exploration-exploitation strategies, it efficiently guides the search through the hyperparameter space, ultimately leading to improved performance and generalization of machine learning models.
Simulated Annealing
Simulated annealing is a widely used and effective optimization algorithm inspired by the annealing process in metallurgy. It is particularly useful for hyperparameter tuning in machine learning, where the objective is to find the optimal set of hyperparameters that maximize model performance.
Simulated annealing mimics the process of physical annealing in which a metal is heated and then slowly cooled, allowing the atoms to settle into a low-energy state. Similarly, in simulated annealing, the algorithm starts with an initial solution, known as the current state, and iteratively explores the neighboring search space by perturbing the current configuration.
The algorithm accepts worse solutions early in the process, providing a mechanism to escape local optima, and gradually becomes more selective as it progresses. This is controlled by a parameter known as the temperature. As the temperature decreases, the algorithm becomes less likely to accept worse solutions, allowing it to converge to an optimal or near-optimal solution.
The perturbation of the current configuration is done by randomly modifying the values of the hyperparameters. The degree of perturbation is controlled by another parameter called the cooling rate. A higher cooling rate leads to more significant changes, allowing the algorithm to explore a larger space, while a lower cooling rate focuses on refining the current solutions.
Simulated annealing inherently provides a balance between exploration and exploitation. In the early stages, the algorithm explores a wide range of hyperparameter configurations, including those that might initially yield worse performance. This ability to accept worse solutions helps simulated annealing to escape local optima and search for better solutions in the hyperparameter space.
One of the advantages of simulated annealing is its ability to handle rugged and complex optimization landscapes. These landscapes may contain multiple peaks and valleys, representing different combinations of hyperparameters with varying performance. The random perturbation of current solutions allows the algorithm to traverse these landscapes and find better hyperparameter configurations in regions that might not be easily explored by other optimization methods.
A crucial aspect of simulated annealing is the temperature schedule. The cooling schedule determines the rate at which the temperature decreases over time. It should be designed carefully to balance exploration and exploitation efficiently. The initial temperature should be sufficiently high to allow for exploration, and the cooling rate should follow a smooth and gradual decrease to ensure adequate convergence to an optimal solution.
While simulated annealing is a powerful optimization algorithm, it may have limitations in high-dimensional hyperparameter spaces. The curse of dimensionality can lead to increased exploration times as the search space grows exponentially with the number of hyperparameters. Dimensionality reduction techniques, such as principal component analysis or feature selection, can help alleviate this issue.
In summary, simulated annealing is an optimization algorithm widely used for hyperparameter tuning. Inspired by the annealing process in metallurgy, it finds optimal or near-optimal combinations of hyperparameters by iteratively exploring and perturbing the current solution. Simulated annealing’s ability to escape local optima and handle complex landscapes makes it a valuable tool in the search for optimal hyperparameters.
Genetic Algorithms
Genetic algorithms are a class of optimization algorithms that draw inspiration from the process of natural selection and genetic variation observed in biological systems. They have been successfully applied to hyperparameter tuning in machine learning, providing an effective way to explore and find optimal hyperparameter configurations.
Genetic algorithms start with an initial population of hyperparameter configurations, which represent potential solutions to the optimization problem. Each configuration, or individual in the population, is evaluated based on its performance using a predefined fitness function or objective metric.
Iteratively, the genetic algorithm applies several genetic operators including selection, crossover, and mutation, to create new offspring from the existing population. The individuals with higher fitness scores are more likely to be selected as parents for reproduction. Through crossover, genetic material is exchanged between selected parents to create new individuals known as offspring.
The genetic algorithm also introduces random perturbations called mutations in the offspring’s genetic information. Mutations add diversity to the population, preventing premature convergence and potentially leading to exploring new regions of the hyperparameter space.
After creating a new population of offspring, the cycle continues, with the fitness evaluation, selection, crossover, and mutation steps being applied iteratively. This process allows the genetic algorithm to evolve and improve the population over generations, gradually converging towards a set of hyperparameters that optimizes the model’s performance.
One of the key advantages of genetic algorithms is their ability to handle large and complex search spaces. By exploring various combinations of hyperparameters, genetic algorithms can effectively navigate rugged landscapes and locate promising areas that can lead to better performance.
Moreover, genetic algorithms exhibit a form of implicit parallelism. Multiple individuals in the population can be evaluated and evolved simultaneously, which can expedite the convergence process and make them suitable for distributed computing environments.
It is important to note that the performance of genetic algorithms heavily depends on the choice of genetic operators, such as selection strategies, crossover techniques, and mutation rates. The selection strategy determines how individuals are selected for reproduction, while the crossover and mutation operations control the exchange and alteration of genetic information.
Genetic algorithms provide a flexible and robust framework for hyperparameter tuning, but they also have some limitations. The computational requirements can be substantial, particularly for large populations and complex models. Additionally, the effectiveness of genetic algorithms may diminish as the dimensionality of the hyperparameter space increases due to the “curse of dimensionality.” In such cases, dimensionality reduction techniques or other optimization methods may be more suitable.
In summary, genetic algorithms are optimization algorithms inspired by biological evolution and natural selection. They provide an effective approach for hyperparameter tuning by evaluating, selecting, reproducing, and mutating hyperparameter configurations to find the optimal set of values. Genetic algorithms excel at handling complex search spaces, but their performance can be affected by the choice of genetic operators and computational requirements.
Automated Machine Learning
Automated Machine Learning (AutoML) has gained significant attention in recent years as a comprehensive solution to the challenges of building machine learning models, including the tuning of hyperparameters. AutoML frameworks aim to automate the entire machine learning pipeline, from data preprocessing and feature selection to model selection and hyperparameter tuning.
AutoML platforms leverage a combination of techniques and algorithms to simplify and streamline the process of building machine learning models. They try to minimize the manual intervention required from the user, allowing even those without extensive expertise in machine learning to benefit from automated and optimized models.
One of the key components of AutoML is automated hyperparameter tuning. These platforms provide mechanisms to automatically search, select, and tune the hyperparameters of different machine learning models. Instead of manually specifying the hyperparameter values, the AutoML system takes care of this process, saving time and effort.
AutoML platforms employ various strategies for hyperparameter tuning. They often combine multiple approaches, such as grid search, random search, Bayesian optimization, or genetic algorithms, to search the hyperparameter space more effectively. Some platforms may also incorporate model-based optimization techniques, ensemble methods, or heuristics to further enhance the tuning process.
The advantage of AutoML is that it abstracts away the technical complexities of machine learning and provides a user-friendly interface for building models. Users can focus on defining the problem, selecting the dataset, and specifying evaluation metrics, while the AutoML system takes care of the details, including hyperparameter tuning.
AutoML frameworks typically provide automatic preprocessing steps, such as handling missing values, feature encoding, and feature scaling. They also automate feature selection, choosing the most informative subset of features from the available options. Additionally, AutoML platforms can automatically try different algorithms and model families to find the one that works best for the given problem.
AutoML is particularly beneficial in scenarios where time is of the essence, or when users lack in-depth knowledge of machine learning concepts and techniques. It enables rapid model development, iteratively refining hyperparameters and experimenting with different settings to find the optimal configuration that maximizes model performance.
However, it is important to note that AutoML is not a one-size-fits-all solution. The performance and capabilities of AutoML platforms can vary depending on the specific implementation and the complexity of the problem. The quality of the results obtained may also depend on the size and quality of the given dataset.
In summary, Automated Machine Learning (AutoML) offers a comprehensive solution for building machine learning models by automating the entire pipeline, including hyperparameter tuning. AutoML platforms abstract away technical complexities and provide user-friendly interfaces, enabling users to build optimized models without deep knowledge of machine learning. Although AutoML can be a powerful tool, its performance and effectiveness depend on the specific implementation and the complexity of the problem at hand.
Best Practices for Tuning
Tuning hyperparameters is a critical step in machine learning to optimize model performance and improve generalization. While there is no one-size-fits-all approach to hyperparameter tuning, following best practices can help ensure a more effective and efficient tuning process. Here are some key best practices to consider:
1. Set a Clear Evaluation Metric: Define a well-defined evaluation metric that aligns with the problem at hand. This metric will guide the tuning process by quantifying the performance of different hyperparameter configurations and allowing for objective comparisons.
2. Select an Appropriate Search Space: Carefully define the range and granularity of the search space for each hyperparameter. Consider domain knowledge, prior experience, and any constraints when determining reasonable values. It’s helpful to perform a preliminary analysis or consult experts to narrow down the search space.
3. Start with Coarse-grained Search: Begin the tuning process with a coarse-grained search that encompasses a wide range of hyperparameter values. This helps quickly identify the general region of the search space that contains good configurations before refining the search around those promising regions.
4. Use Validation Data: Split the dataset into training, validation, and test sets. Use the validation set to evaluate the performance of different hyperparameter configurations during the tuning process. Avoid using the test set until the final model is chosen to avoid overfitting on the test set.
5. Implement Cross-Validation: Utilize techniques like k-fold cross-validation during the tuning process. Cross-validation provides a more reliable estimate of model performance by evaluating the model on multiple subsets of the data, reducing the risk of overfitting and improving generalizability.
6. Prioritize Promising Configurations: As the tuning process progresses, focus on the hyperparameter configurations that show promise. Prioritize their evaluation to allocate more computational resources to potentially fruitful regions of the search space.
7. Avoid Tuning Too Many Hyperparameters Simultaneously: Tuning a large number of hyperparameters simultaneously can lead to a combinatorial explosion of configurations, making the tuning process more challenging and computationally expensive. Prioritize the most impactful hyperparameters or consider techniques such as dimensionality reduction or feature selection to reduce the number of hyperparameters.
8. Utilize Parallelization if Possible: Exploit the parallelizability of the tuning process by distributing the evaluation of different hyperparameter configurations across multiple processors or machines. This can significantly speed up the tuning process, particularly for computationally expensive models or large datasets.
9. Regularly Monitor and Record Results: Keep track of the performance of evaluated hyperparameter configurations throughout the tuning process. Maintaining a log of results helps identify patterns, draw insights, and learn from previous evaluations, enabling more informed decisions as the tuning progresses.
10. Tweak Final Configuration: After selecting the optimal hyperparameter configuration based on the validation set’s performance, further fine-tune the chosen configuration if time and resources allow. This final tweaking can involve testing small adjustments to the selected values to squeeze out additional performance gains.
Remember that hyperparameter tuning is an iterative and resource-intensive process. It requires patience, experimentation, and careful analysis. Following these best practices along with domain knowledge and intuition can significantly enhance the effectiveness of hyperparameter tuning, resulting in improved model performance and generalization.
Conclusion
Tuning hyperparameters is a crucial step in machine learning to optimize model performance and achieve better generalization. With the availability of various tuning methods, including grid search, random search, Bayesian optimization, simulated annealing, genetic algorithms, and automated machine learning, finding the optimal set of hyperparameters has become more accessible and efficient.
Each tuning method has its advantages and considerations. Grid search provides a comprehensive search of the hyperparameter space, while random search offers a more efficient alternative. Bayesian optimization leverages probabilistic models to guide the search process, and simulated annealing mimics the annealing process to escape local optima. Genetic algorithms mimic natural selection and genetic variation, and automated machine learning platforms automate the entire machine learning pipeline, including hyperparameter tuning.
Regardless of the chosen method, there are best practices to consider, such as setting clear evaluation metrics, selecting appropriate search spaces, utilizing validation data and cross-validation, prioritizing promising configurations, and avoiding tuning too many hyperparameters simultaneously. Regular monitoring and recording of results, parallelization if possible, and final tweaking of the chosen configuration are also valuable practices to follow.
Hyperparameter tuning is an iterative process that requires careful experimentation, assessment, and adjustment. It is essential to strike a balance between exploration and exploitation, taking into account the specific problem, dataset, and resources available. By dedicating time and effort to tuning, machine learning models can achieve optimal performance, maximize accuracy, and improve generalization on new, unseen data.
Overall, hyperparameter tuning plays a crucial role in unlocking the full potential of machine learning models. It enhances their performance, robustness, and reliability, ensuring that they are suited to specific problems and datasets. By incorporating the best practices and leveraging the available tuning methods, practitioners can optimize their machine learning models and stay at the forefront of the ever-evolving field of artificial intelligence.