Introduction
An activation function is a critical component in the field of machine learning and neural networks. It plays a crucial role in determining the output of a computational unit or a node in a neural network. Activation functions introduce non-linearity into the network, allowing it to learn complex patterns and make accurate predictions.
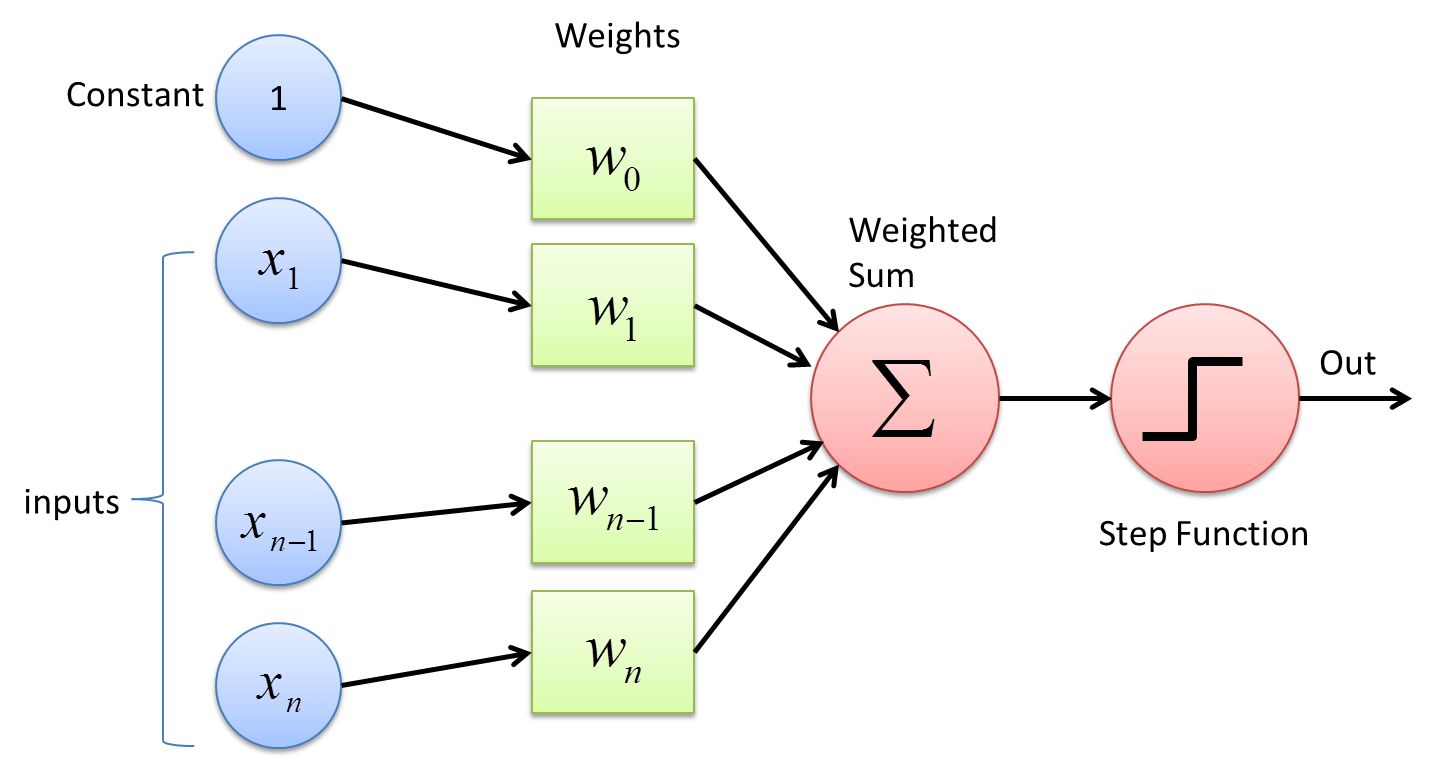
Simply put, an activation function takes the weighted sum of inputs from the previous layer, applies a certain mathematical operation to it, and outputs the result to the next layer. The choice of activation function can significantly impact the performance and efficiency of a machine learning model.
Activation functions serve the purpose of introducing non-linear transformations, which enable the network to learn complex relationships and map inputs to the desired output. They act as a decision-making mechanism, determining whether the output of a neuron should be activated or not.
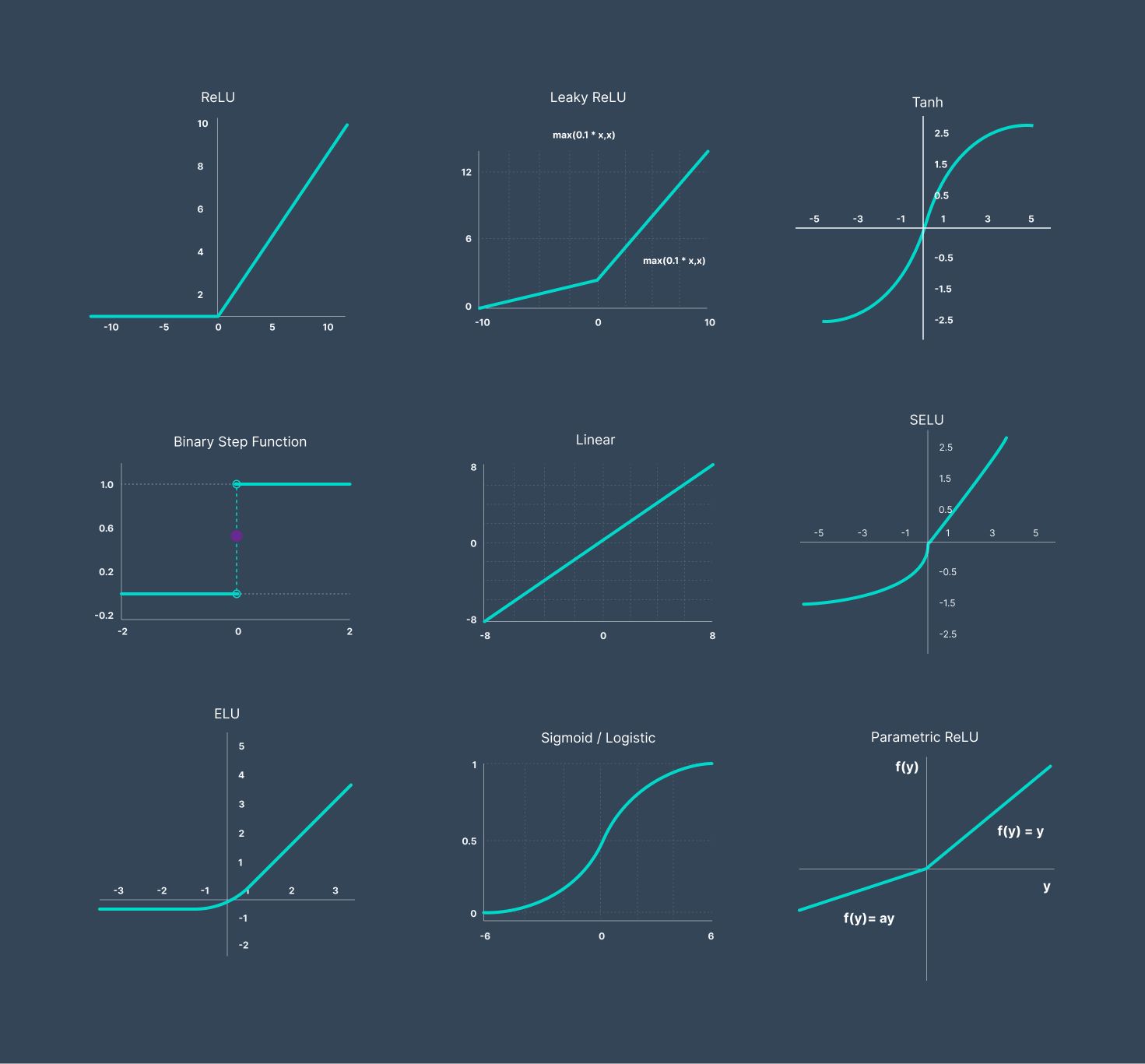
There are various activation functions available, each with its own characteristics and suitable applications. Some popular activation functions include the sigmoid function, step function, rectified linear unit (ReLU), and hyperbolic tangent (tanh) function. These functions have different mathematical properties and impact the behavior of the neural network in unique ways.
The choice of activation function depends on the nature of the problem, the type of data, and the desired output of the model. It is important to select an appropriate activation function to ensure that the neural network can effectively learn and generalize patterns from the input data.
In this article, we will explore the different types of activation functions and discuss their advantages, disadvantages, and use cases. Understanding the role and characteristics of activation functions is essential for building effective machine learning models, and this article will serve as a guide to help you make informed decisions when implementing neural networks.
Definition of Activation Function
An activation function is a mathematical function that introduces non-linearity into a neural network. It determines the output of a neuron based on the weighted sum of inputs from the previous layer. By applying an activation function, the neural network can learn and represent complex, non-linear relationships between inputs and outputs.
The activation function takes the weighted sum of inputs, which is also known as the activation level or net input, and applies a specific transformation to it. This transformation introduces non-linear properties to the output, allowing the neural network to process and learn complex data patterns. Without the activation function, the neural network would only be able to learn linear relationships and would not be able to perform tasks that require non-linear mappings.
Activation functions can be classified into two types: binary activation functions and continuous activation functions. Binary activation functions, such as the step function, produce a binary output based on a threshold. If the net input is above the threshold, the output is one, representing activation; otherwise, the output is zero, representing deactivation. On the other hand, continuous activation functions, such as the sigmoid function, produce a continuous output that ranges between zero and one or between -1 and 1.
Activation functions play a vital role in the learning process of neural networks. During the training phase, the weights of the network adjust to minimize the error between the predicted output and the actual output. The choice of activation function affects the convergence speed and the accuracy of the model. An appropriate activation function enables the network to effectively learn and generalize patterns from the input data. Different activation functions have different characteristics and can be used depending on the specific problem and requirements of the neural network.
In the next sections, we will explore some popular activation functions and discuss their properties, advantages, and use cases in machine learning.
Purpose of Activation Function
The purpose of an activation function in machine learning and neural networks is to introduce non-linearity into the network. By applying a non-linear activation function, neural networks are able to learn complex patterns and make accurate predictions.
One of the key advantages of using activation functions is that they allow neural networks to approximate any continuous function. Without an activation function, the neural network would simply be a linear model, capable only of learning linear relationships between inputs and outputs. However, for most real-world problems, linear models are insufficient, as the relationships between variables are often non-linear and complex.
Activation functions serve as a decision-making mechanism for the network, determining whether the output of a neuron should be activated or not. They introduce non-linear transformations to the output of a neuron, enabling the network to learn and represent non-linear relationships between input and output variables. This non-linearity is crucial for capturing more complex patterns and making accurate predictions.
Another purpose of activation functions is to control the output range of neurons. Different activation functions have different output ranges, which can be useful in different scenarios. For example, the sigmoid function outputs values between 0 and 1, which can be interpreted as probabilities. This is particularly useful in binary classification tasks, where the output represents the probability of belonging to a certain class. On the other hand, the hyperbolic tangent function (tanh) outputs values between -1 and 1, which can be helpful in tasks where negative values carry meaning.
The choice of activation function depends on the nature of the problem and the desired behavior of the neural network. Some activation functions, such as the sigmoid and hyperbolic tangent, introduce smooth non-linearity, while others, like the rectified linear unit (ReLU), introduce piecewise linear behavior. The characteristics of the activation function can impact the convergence of the neural network and the speed at which it learns. Different activation functions also have different computational costs, which should be taken into consideration when designing and training neural networks.
In the next sections, we will explore some popular activation functions and discuss their strengths, weaknesses, and use cases in machine learning.
Popular Activation Functions
There are several popular activation functions used in machine learning and neural networks, each with its own characteristics and suitability for different applications. In this section, we will explore some of these activation functions and discuss their strengths and weaknesses.
Sigmoid Function:
The sigmoid function is one of the oldest activation functions and is commonly used in binary classification problems. It maps the input to a value between 0 and 1, which can be interpreted as a probability. The sigmoid function’s smoothness allows for a gentle transition between the two extremes, making it useful for gradient-based optimization algorithms. However, the sigmoid function suffers from the vanishing gradients problem, where large input values result in small gradients, hindering the learning process.
Step Function:
The step function is a simple activation function that outputs either 0 or 1 based on a threshold. It is often used in binary classification problems or when dealing with binary data. While the step function can be useful in simple tasks, its discontinuous nature poses challenges for optimization algorithms that rely on gradients. Additionally, the step function’s inability to capture gradual changes limits its effectiveness in more complex tasks.
Rectified Linear Unit (ReLU):
The rectified linear unit, commonly known as ReLU, has gained popularity in recent years. It maps all negative inputs to zero and keeps positive inputs unchanged. ReLU offers several advantages, including computational efficiency and the ability to mitigate the vanishing gradient problem. It is widely used in deep learning models and has shown to be effective in improving training speed and accuracy. However, ReLU can suffer from the dying ReLU problem, where a large number of neurons become inactive and output zero, impacting the network’s capacity to learn.
Hyperbolic Tangent Function (Tanh):
The hyperbolic tangent function, or tanh, maps the input to a value between -1 and 1. It is similar to the sigmoid function but centered around zero. Tanh possesses the advantages of sigmoid, including smoothness and suitability for binary classification tasks. However, unlike sigmoid, tanh has a symmetric range, allowing negative outputs. Tanh can be useful in situations where negative values carry meaning, but it still suffers from the vanishing gradient problem for large input values.
These activation functions are just a few examples of what is available in the field of machine learning. Each function has its unique characteristics and is suitable for different types of problems. The choice of activation function requires careful consideration, taking into account the specific requirements of the task and the network architecture.
Sigmoid Function
The sigmoid function, also known as the logistic function, is a popular activation function used in neural networks. It is a smooth, S-shaped curve that maps the input to a value between 0 and 1. The sigmoid function is often used in binary classification problems where the output represents the probability of belonging to a certain class.
The mathematical formula for the sigmoid function is:
σ(x) = 1 / (1 + e^-x)
Where σ(x) is the output of the sigmoid function and x is the input value.
One of the main advantages of the sigmoid function is its differentiability, which allows it to be used in gradient-based optimization algorithms for training neural networks. The smoothness of the curve enables a gentle transition between the two extremes, making it suitable for tasks where gradual changes are important.
However, the sigmoid function does have its limitations. One significant drawback is the vanishing gradients problem. For large input values, the derivative of the sigmoid function becomes close to zero, resulting in small gradients. This can cause difficulties in training deep neural networks, as the gradients become too small to effectively update the weights and biases of the network.
Moreover, the output of the sigmoid function is not symmetric around zero since it is restricted to the range of 0 to 1. This lack of symmetry may not be suitable for tasks where negative values carry meaning.
Despite these limitations, the sigmoid function remains a commonly used activation function, particularly in the early stages of neural network research and binary classification problems. Its smoothness and interpretability make it a popular choice, especially when the output needs to be interpreted as probabilities.
In practice, it is important to consider the limitations of the sigmoid function and experiment with other activation functions, such as ReLU or tanh, to improve the performance and convergence of the neural network for different tasks and architectures.
Step Function
The step function is a simple and straightforward activation function that maps its input to either 0 or 1 based on a threshold. It is commonly used in binary classification tasks or when dealing with binary data.
The step function can be defined as follows:
f(x) = 0, if x <= 0
f(x) = 1, if x > 0
Where f(x) is the output of the step function and x is the input value.
Unlike other activation functions that introduce non-linearity, the step function is discontinuous and only produces two possible outputs. If the input is less than or equal to zero, the output is zero, indicating deactivation. If the input is greater than zero, the output is one, indicating activation.
While the step function is simple to understand and implement, it has certain limitations. The main drawback of the step function is its inability to capture gradual changes in the input. The output abruptly changes from 0 to 1 at the threshold, resulting in a discontinuous behavior. This discontinuity makes it problematic to use the step function in optimization algorithms that rely on calculating gradients such as backpropagation.
Despite its limitations, the step function still finds applications in specific scenarios. For instance, it can be useful in simple binary classification tasks where only a clear decision of activating or deactivating is needed. Additionally, the step function is often used as a building block for constructing more complex activation functions or as an element in artificial neural networks that utilize threshold gates.
Overall, while the step function’s simplicity can be advantageous in some cases, its inability to capture gradual changes and the discontinuous nature make it less suitable for more complex tasks. Other activation functions, such as the sigmoid, ReLU, or tanh, offer smoother transitions and better gradients, making them more commonly used in modern neural network architectures.
Rectified Linear Unit (ReLU)
The Rectified Linear Unit, commonly known as ReLU, is one of the most popular activation functions used in deep learning models. It offers several advantages over other activation functions, making it a go-to choice for many neural network architectures.
The ReLU function can be defined as follows:
f(x) = max(0, x)
Where f(x) is the output of the ReLU function and x is the input value.
ReLU is a piecewise linear function that sets all negative input values to zero, keeping the positive input values unchanged. This results in a rectified output that tends to be linear for positive values and zero for negative values.
ReLU has several advantages that contribute to its popularity. Firstly, it avoids the vanishing gradient problem that affects activation functions such as the sigmoid or tanh. The derivative of ReLU is either 0 or 1, depending on the input value, which helps in maintaining more substantial gradients during backpropagation and improving the training process of deep neural networks.
Secondly, ReLU is computationally efficient. The ReLU activation function involves simple operations, such as the comparison and selection of values, making it faster compared to activation functions that involve more complex calculations, such as exponentiation in the sigmoid or tanh functions.
However, ReLU is not without its limitations. One drawback is the potential for dead neurons or the “dying ReLU” problem. When a neuron is in the zero-activated state (outputting zero) for a long time during training, the neuron may become “dead” and cease to learn. This issue is typically mitigated using initialization techniques or variants of ReLU, such as Leaky ReLU or Parametric ReLU.
Despite its limitations, ReLU has become an industry standard for many deep learning models. Its simplicity, computational efficiency, and ability to alleviate the vanishing gradient problem make it a reliable choice for a wide range of tasks, including image classification, object detection, and natural language processing.
Overall, ReLU has proven to be an effective activation function in deep learning models, providing improved training performance and better generalization capabilities in a computationally efficient manner.
Hyperbolic Tangent Function (Tanh)
The hyperbolic tangent function, commonly referred to as tanh, is another commonly used activation function in machine learning and neural networks. It is a continuous, sigmoid-shaped function that maps the input to values between -1 and 1. Tanh is similar to the sigmoid function but is centered around zero, resulting in an output range that includes negative values.
The mathematical expression for the hyperbolic tangent function is:
tanh(x) = (e^x - e^-x) / (e^x + e^-x)
Where tanh(x) is the output of the tanh function and x is the input value.
Tanh shares some similarities with the sigmoid function, including smoothness and suitability for binary classification tasks. However, unlike the sigmoid function, the tanh function produces outputs that range from -1 to 1, allowing negative values. This can be valuable in tasks where both positive and negative outputs carry significance or when data exhibits a symmetrical distribution around zero.
Similar to the sigmoid function, tanh suffers from the vanishing gradients problem. For extremely large input values, the derivative approaches zero, resulting in small gradients and potentially hindering the learning process. However, tanh still offers better gradient behavior compared to the sigmoid function, as it manifests steeper slopes around zero.
One important characteristic of the tanh function is that it is an odd function. This means that tanh(-x) = -tanh(x). This property makes it useful in certain situations, such as when you want to preserve the sign of the input while applying a non-linear transformation.
Tanh activation is commonly used in recurrent neural networks (RNNs) for tasks such as language modeling and sentiment analysis. Its ability to capture both positive and negative values makes it well-suited for tasks that involve sentiment analysis, where positive and negative sentiments need to be distinguished.
While tanh has its limitations, it remains a valuable activation function option, especially when dealing with tasks that require capturing both positive and negative values. However, like with any activation function, it is essential to consider its characteristics and compare it with other alternatives to select the most suitable activation function for your specific problem and neural network architecture.
Comparison of Activation Functions
Choosing the right activation function is crucial for building effective machine learning models. In this section, we will compare some popular activation functions and discuss their strengths, weaknesses, and use cases.
Sigmoid Function:
The sigmoid function is commonly used in binary classification tasks where the output needs to be interpreted as probabilities. It offers a smooth transition between the two extremes and is differentiable, making it suitable for gradient-based optimization algorithms. However, sigmoid suffers from the vanishing gradients problem and is computationally more expensive compared to other activation functions.
Step Function:
The step function is simple and easy to implement, making it suitable for simple binary classification tasks or when dealing with binary data. However, its discontinuous nature limits its use in optimization algorithms that rely on gradients. It is not suitable for tasks that require capturing gradual changes in the input.
Rectified Linear Unit (ReLU):
ReLU offers computational efficiency and mitigates the vanishing gradient problem. It is widely used in deep learning models and has shown improved training speed and performance. However, ReLU can suffer from the dying ReLU problem, where some neurons become inactive and cease to learn.
Hyperbolic Tangent Function (Tanh):
Tanh provides outputs in the range of -1 to 1, capturing both positive and negative values. It is useful in tasks where negative values carry meaning or when data exhibits a symmetrical distribution around zero. However, tanh also suffers from the vanishing gradients problem, particularly for large input values.
The choice of activation function depends on the nature of the problem and the desired behavior of the neural network. For binary classification tasks, sigmoid or tanh may be suitable. If efficiency and training speed are important, ReLU is a common choice. It is also common to use a combination of different activation functions in different layers of the neural network to leverage their respective advantages.
It is important to experiment and compare the performance of different activation functions in your specific task to identify the optimal choice. Additionally, advancements in deep learning research have led to the development of various variants and hybrid activation functions that aim to address the limitations of existing ones.
Consider the specific characteristics of your problem and the behaviors that the activation functions offer to ensure that they align with the requirements of your neural network model.
Conclusion
Activation functions play a vital role in machine learning and neural networks, enabling them to learn and represent complex patterns by introducing non-linearity. In this article, we explored various popular activation functions, including the sigmoid function, step function, rectified linear unit (ReLU), and hyperbolic tangent (tanh) function.
The sigmoid function is commonly used in binary classification tasks, while the step function is suitable for simple binary decision problems. ReLU offers computational efficiency and addresses the vanishing gradients problem but may suffer from the dying ReLU problem. Tanh captures both positive and negative values, making it useful in tasks where negative values carry meaning or when data exhibits a symmetrical distribution around zero. However, tanh shares the vanishing gradients problem with sigmoid.
In selecting the appropriate activation function, considerations should be given to the problem’s nature, desired behavior of the neural network, and computational efficiency. It is also important to note that no single activation function is universally superior, and their effectiveness may vary depending on the specific task and network architecture.
Further advancements in research have led to the development of new activation functions and variants that aim to overcome the limitations of existing ones. Experimentation and comparison of different activation functions are essential to identify the most suitable one for a specific machine learning task.
Overall, understanding the characteristics and strengths of activation functions is crucial for building effective machine learning models. By selecting the right activation function, researchers and practitioners can enhance the learning capacity, convergence speed, and generalization capabilities of their neural networks.