What Is Clustering In Machine Learning

Introduction

Welcome to the world of machine learning, where algorithms and data analysis have revolutionized the way we process information and make decisions. One crucial aspect of machine learning is clustering, a technique that groups similar objects or data points together. Clustering plays a pivotal role in uncovering patterns, insights, and relationships within datasets, enabling us to make informed predictions and gain valuable knowledge.

Clustering is not a new concept; humans have been categorizing things based on similarities for centuries. Just think about how we group animals based on their characteristics or how we classify books in a library based on their genres. Machine learning extends this idea to automatically identify patterns and group data points based on their features or attributes.

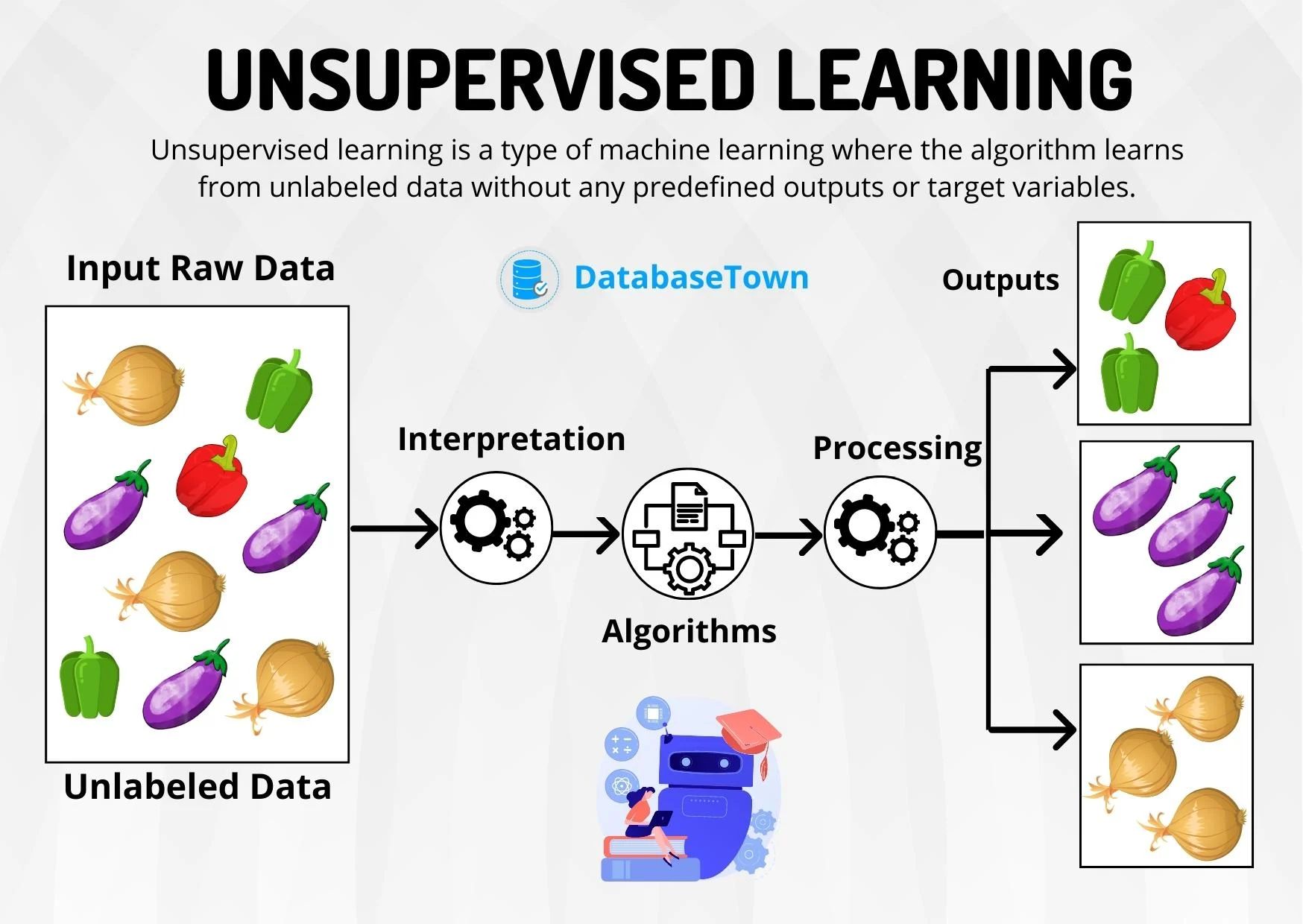
The primary objective of clustering is to identify inherent structures or clusters within a dataset without any prior knowledge or labels. Unlike supervised learning, where the algorithm is trained on labeled data, clustering is an unsupervised learning technique. It infers patterns and relationships purely based on the inherent properties of the data.

By identifying clusters in a dataset, machine learning algorithms can uncover hidden structures, discover anomalies or outliers, segment customers based on their preferences, and even recommend relevant products or services.

The process of clustering involves assigning data points to different groups based on their similarity or dissimilarity. The goal is to maximize the similarity within each cluster while minimizing the similarity between different clusters. This can be achieved through various clustering algorithms, each with its own strengths and weaknesses.

In this article, we will explore the fundamentals of clustering in machine learning. We will delve into the importance of clustering, the common clustering algorithms, how to evaluate clustering performance, and the real-world applications where clustering plays a vital role. So, let’s dive in and unravel the secrets behind this powerful machine learning technique!

What is Clustering?

Clustering, in the context of machine learning, is a technique used to group similar objects or data points together based on their characteristics or attributes. It is a fundamental unsupervised learning task that aims to identify hidden structures or patterns within a dataset without any prior knowledge or labels.

The process of clustering involves partitioning the data into subsets, known as clusters, such that the objects within each cluster are more similar to each other than to those in other clusters. The similarity or dissimilarity between data points is determined using distance metrics, such as Euclidean distance or cosine similarity.

There are various types of clustering techniques, each with its own approach and assumptions. Some clustering algorithms rely on defining the number of clusters in advance, while others automatically determine the optimal number of clusters based on the data’s inherent structure.

Clustering algorithms are based on different principles, such as distance-based clustering, density-based clustering, and hierarchical clustering. Each algorithm has its own advantages and limitations, making it suitable for different types of datasets and applications.

Clustering can be applied to a wide range of domains, including image recognition, customer segmentation, anomaly detection, text mining, and recommendation systems. In image recognition, clustering can be used to group similar images together, aiding in tasks such as image retrieval and classification. Customer segmentation allows businesses to identify distinct groups of customers with similar preferences and behaviors, enabling targeted marketing strategies. Anomaly detection using clustering can help identify unusual patterns or outliers, such as fraudulent transactions. In text mining, clustering can be used to group similar documents together, facilitating document organization and retrieval. Recommendation systems often leverage clustering to group users with similar interests and make personalized recommendations.

Clustering is a versatile technique that uncovers valuable insights and patterns in data. It helps in understanding the underlying structure and relationships, which can lead to more effective decision-making processes. By grouping similar data points together, clustering allows us to analyze and interpret large datasets more efficiently, making it an indispensable tool in the field of machine learning.

Why is Clustering Important in Machine Learning?

Clustering is a crucial technique in machine learning that offers numerous benefits and plays a vital role in various applications. Let’s explore why clustering is important:

1. Data Exploration and Understanding: Clustering helps in exploring and understanding data by revealing inherent structures and patterns. It allows us to gain insights into the relationships and similarities between data points, providing a deeper understanding of the data. By visualizing the clusters, we can identify groups with similar characteristics and evaluate the distribution of data.

2. Finding Anomalies or Outliers: Clustering can identify anomalies or outliers in a dataset. Outliers are data points that significantly deviate from the norm or expected patterns. By clustering the data, outliers can be identified as data points that do not belong to any cluster or are in clusters of very small size. This is valuable for detecting fraudulent transactions, identifying manufacturing defects, or spotting unusual behaviors.

3. Customer Segmentation: Clustering is widely used in marketing and customer analysis to segment customers based on their preferences, behaviors, or demographic characteristics. Understanding customer segments enables businesses to tailor their products, marketing strategies, and services to specific customer groups, resulting in improved customer satisfaction and higher conversion rates.

4. Image and Document Organization: Clustering can help organize large collections of images or documents by grouping similar ones together. This aids in image or document retrieval, content recommendation, and categorization. Clustering allows us to navigate through vast amounts of visual or textual data more efficiently, making it easier to find relevant information.

5. Feature Engineering: Clustering can be used as a preprocessing step for feature engineering. By clustering similar data points, we can create new features that capture the underlying patterns or relationships within the data. These new features can then be used as inputs for machine learning models, enhancing their performance and prediction accuracy.

6. Dimensionality Reduction: Clustering can be used for dimensionality reduction by identifying the most representative data points within each cluster. Instead of working with the entire dataset, we can select a subset of representative points from each cluster. This reduces the computational complexity and memory requirements while preserving the essential information contained in the data.

Overall, clustering is essential in machine learning as it helps in data exploration, anomaly detection, customer segmentation, image and document organization, feature engineering, and dimensionality reduction. By leveraging the power of clustering algorithms, machine learning models can achieve better performance, provide valuable insights, and optimize decision-making processes.

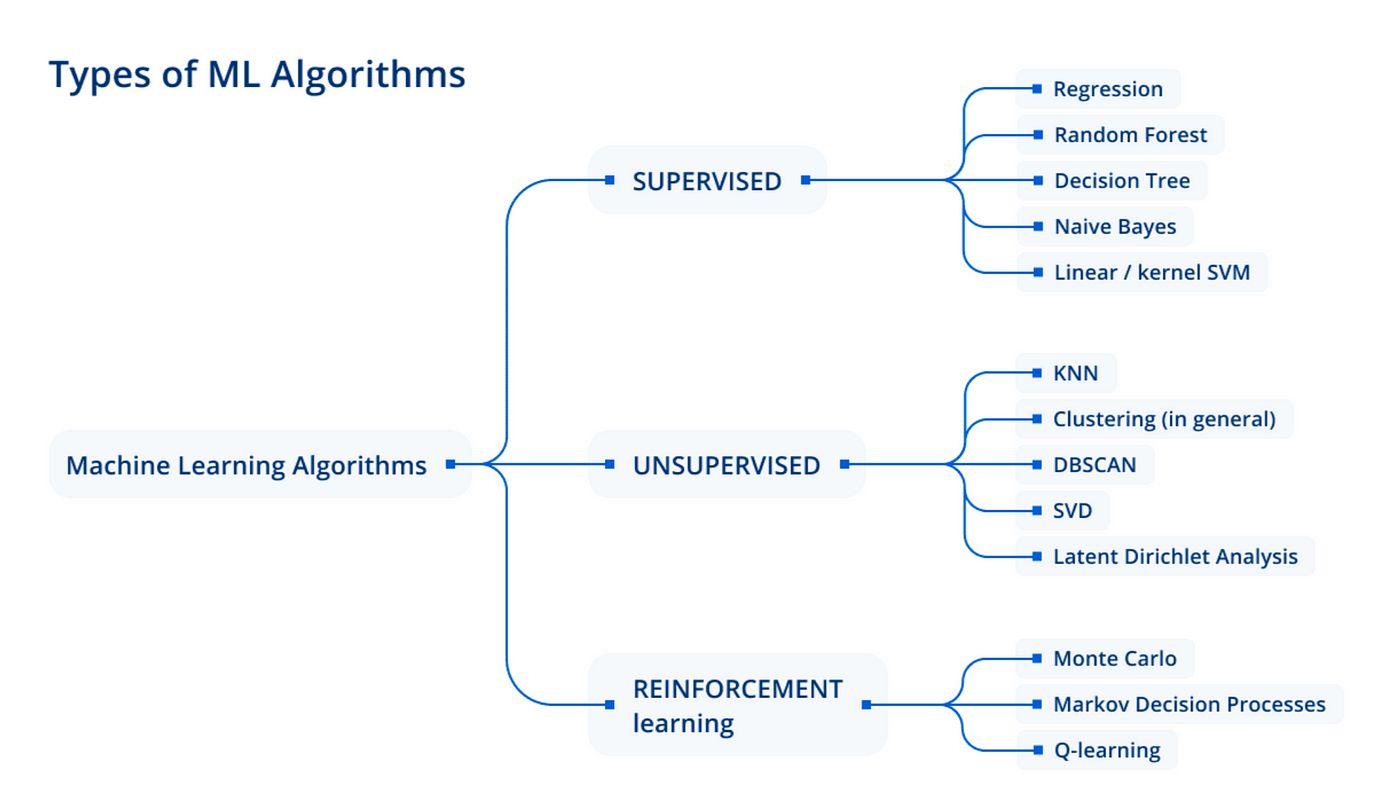
Common Clustering Algorithms

There are several commonly used clustering algorithms, each with its own approach and assumptions. Let’s explore some of the popular clustering algorithms:

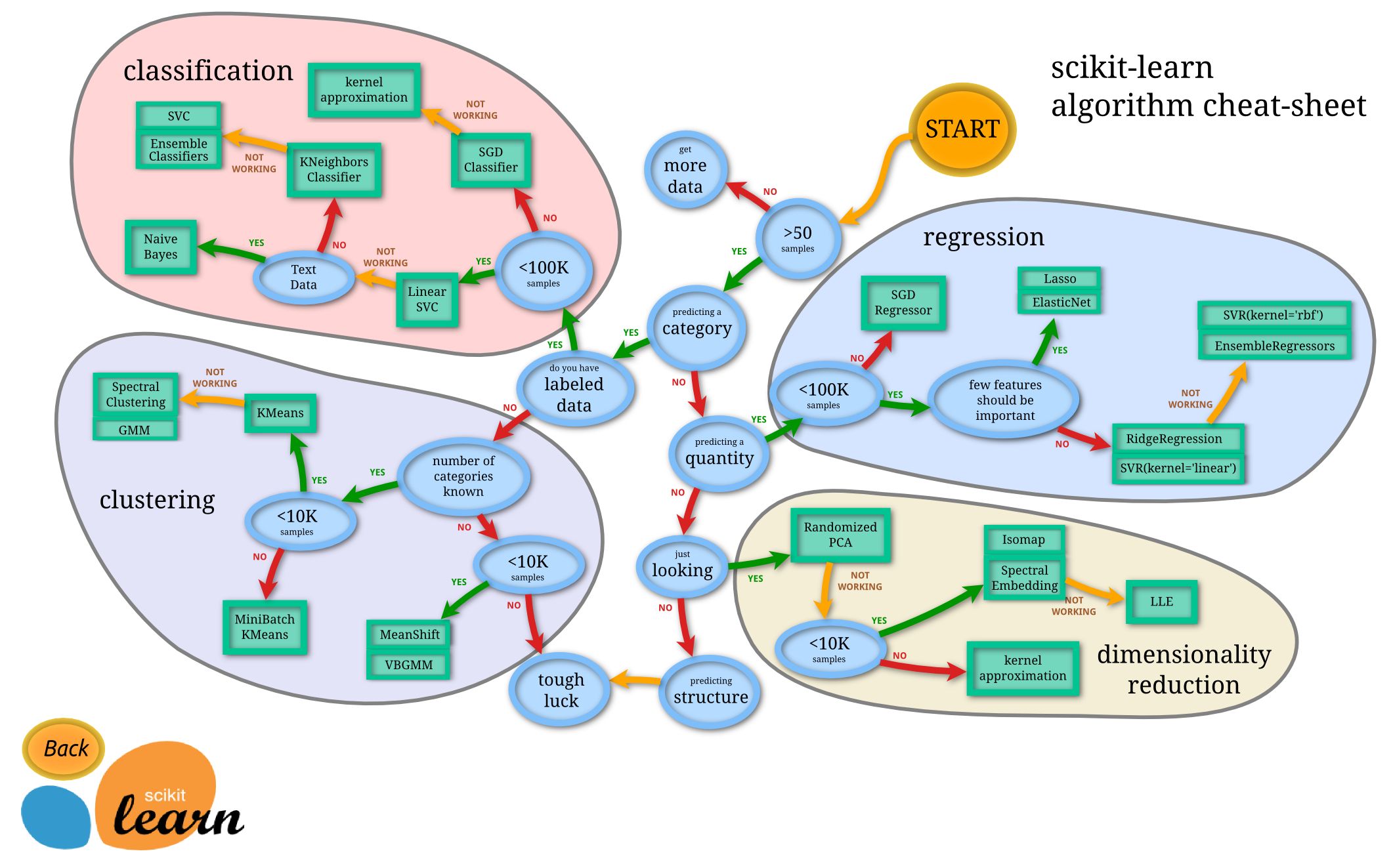
1. K-Means Clustering: K-means clustering is a distance-based algorithm that aims to partition data into K clusters, where K is a pre-defined number. The algorithm iteratively assigns data points to clusters by minimizing the sum of squared distances between the data points and their cluster centroids. K-means clustering is efficient and widely used due to its simplicity and scalability.

2. Hierarchical Clustering: Hierarchical clustering involves creating a hierarchy of clusters by iteratively merging or splitting clusters based on their similarity. Agglomerative hierarchical clustering starts with each data point as a separate cluster and recursively merges clusters until a stopping criterion is met. Divisive hierarchical clustering starts with all data points in a single cluster and recursively splits clusters until each data point forms its own cluster.

3. Density-Based Clustering: Density-based clustering algorithms, such as DBSCAN (Density-Based Spatial Clustering of Applications with Noise), identify clusters based on regions of high density separated by regions of low density. DBSCAN groups together data points that are close to each other and have a sufficient number of neighboring points within a specified radius.

4. Mean-Shift Clustering: Mean-shift clustering is a non-parametric iterative algorithm that finds clusters by shifting data points towards the mode of the kernel density estimate. It identifies clusters as the regions where data points converge. Mean-shift clustering does not require specifying the number of clusters in advance and can detect clusters of different shapes and sizes.

5. Gaussian Mixture Models (GMM): In Gaussian mixture models, data points are assumed to be generated from a mixture of Gaussian distributions. The algorithm aims to estimate the parameters of the Gaussian distributions to identify the underlying clusters. GMM clustering allows for probabilistic assignment of data points to multiple clusters, accommodating data points that belong to more than one cluster.

6. Spectral Clustering: Spectral clustering combines graph theory and linear algebra to cluster data points based on the spectral properties of their similarity matrix. It transforms the data into a lower-dimensional space using eigenvectors and then applies K-means or another clustering algorithm to partition the transformed data into clusters. Spectral clustering is effective for non-linearly separable data and can handle complex structures.

These are just a few examples of the commonly used clustering algorithms in machine learning. Each algorithm has its strengths and weaknesses, making it suitable for different types of datasets and applications. The choice of clustering algorithm depends on factors such as the nature of the data, the desired number of clusters, and the presence of any specific assumptions or requirements.

K-Means Clustering

K-means clustering is a popular distance-based clustering algorithm that aims to partition a dataset into K clusters, where K is a pre-defined number. The algorithm iteratively assigns data points to clusters by minimizing the sum of squared distances between each data point and its cluster centroid.

The steps of the K-means algorithm are as follows:

1. Initialization: Randomly select K initial cluster centroids.
2. Assignment: Assign each data point to the nearest centroid based on the Euclidean distance.
3. Update: Recalculate the centroids of each cluster based on the mean of the data points assigned to that cluster.
4. Repeat: Iterate steps 2 and 3 until convergence, where convergence is achieved when the centroids no longer move significantly or a maximum number of iterations is reached.

The algorithm aims to find the optimal cluster centroids that minimize the within-cluster sum of squared errors (WCSS), also known as the objective function. The WCSS measures the compactness of each cluster and represents the sum of squared distances between each data point and its centroid within a cluster.

K-means clustering has several advantages:

• Efficiency: K-means is computationally efficient, making it suitable for large datasets and high-dimensional data.
• Simplicity: The simplicity of the algorithm makes it easy to implement and interpret.
• Scalability: The algorithm can efficiently handle a large number of data points and clusters.

However, K-means clustering also has some limitations:

• Sensitivity to Initialization: The final clustering result can be sensitive to the initial random selection of cluster centroids. Different initializations can lead to different clustering results.
• Dependence on K: The algorithm requires specifying the number of clusters, K, in advance, which can be a challenge if the optimal number of clusters is unknown.
• Assumption of Equal Cluster Sizes and Variances: K-means assumes that the clusters have equal sizes and variances, which may not hold in some real-world datasets.

K-means clustering finds various applications across different domains. It can be used for customer segmentation, image compression, anomaly detection, and data preprocessing for other machine learning tasks. Additionally, K-means clustering can serve as a foundation for more advanced clustering algorithms or as a starting point for further analysis.

Overall, K-means clustering is a powerful and widely used algorithm that efficiently partitions datasets into K clusters. It provides an effective means of exploring and understanding data patterns, enabling various applications in machine learning and data analysis.

Hierarchical Clustering

Hierarchical clustering is a versatile clustering algorithm that creates a hierarchy of clusters by iteratively merging or splitting clusters based on their similarity. This algorithm does not require a predetermined number of clusters, allowing for a flexible and exploratory approach to clustering.

There are two main types of hierarchical clustering:

1. Agglomerative Hierarchical Clustering: This is a bottom-up approach where each data point starts as a separate cluster, and at each iteration, the algorithm merges the two closest clusters based on a chosen distance metric. The process continues until all data points are in a single cluster or a predefined stopping criterion is met, resulting in a hierarchy of clusters.
2. Divisive Hierarchical Clustering: This is a top-down approach where all data points are considered to be in a single cluster initially. At each iteration, the algorithm splits the cluster that maximizes the distance between its data points. The process continues until each data point forms its own cluster or a stopping criterion is satisfied.

Hierarchical clustering builds a dendrogram, which is a tree-like structure that represents the hierarchy of clusters. The dendrogram can be visualized and used to interpret the clustering results.

The choice of distance metric and linkage criterion is crucial for hierarchical clustering. The distance metric determines how similarity or dissimilarity between clusters or data points is calculated, while the linkage criterion defines how the distances between clusters are used to decide which clusters to merge or split. Common distance metrics include Euclidean distance, Manhattan distance, and cosine similarity. Popular linkage criteria include complete linkage, which merges clusters based on the maximum distance between data points in different clusters, and average linkage, which considers the average distance between data points.

Hierarchical clustering has several advantages:

• Flexibility: Hierarchical clustering allows for exploratory data analysis by providing a hierarchical structure that can be cut at different levels to obtain various clustering solutions.
• Interpretability: The dendrogram provides a visual representation of the clusters, allowing for easy interpretation and understanding of the relationships between data points.
• No Need for Specifying the Number of Clusters: Hierarchical clustering does not require specifying the number of clusters in advance, making it suitable for datasets where the optimal number of clusters is unknown.

However, hierarchical clustering also has some limitations:

• Computationally Expensive: Hierarchical clustering can be computationally expensive, especially for large datasets, due to its iterative nature.
• Limited Scalability: The algorithm’s memory requirements increase with the square of the number of data points, which can make it impractical for datasets with a large number of observations.
• Sensitivity to Noise and Outliers: As the algorithm progressively merges or splits clusters, it can be sensitive to noise or outliers, leading to suboptimal clustering results.

Hierarchical clustering finds applications in various fields, including biology, social sciences, and market research. It can be used to identify genetic subgroups in genomic data, analyze social networks, cluster customers based on their preferences, or group documents based on textual similarities.

In summary, hierarchical clustering is a flexible and interpretable algorithm that creates a hierarchy of clusters based on data similarities. It provides a valuable tool for exploratory data analysis and facilitates the understanding and interpretation of complex datasets.

Density-Based Clustering

Density-based clustering is a clustering algorithm that identifies clusters based on regions of high data point density separated by regions of low density. Unlike distance-based algorithms that require defining the number of clusters in advance, density-based algorithms can automatically discover the number of clusters present in the data.

One popular density-based clustering algorithm is DBSCAN (Density-Based Spatial Clustering of Applications with Noise). DBSCAN groups together data points that are close to each other and have a sufficient number of neighboring points within a specified radius, known as the epsilon parameter. The algorithm defines density-reachable and density-connected relationships between data points to identify clusters.

DBSCAN operates as follows:

1. Core Points: Identify core points by counting the number of data points within the epsilon radius. Core points have at least a specified minimum number of neighbors.
2. Directly Density-Reachable: Determine which non-core points are directly density-reachable from core points by checking if they fall within the epsilon radius of any core point.
3. Density-Connected: Connect data points that are density-reachable from the same core point or density-reachable from another data point forming a path of density-reachable points.
4. Clusters: Assign each data point to a cluster based on its density-connected component. Outliers or noise are considered as unassigned data points.

Density-based clustering has some advantages:

• No Need to Specify the Number of Clusters: Density-based algorithms can automatically determine the number of clusters in the data, making them suitable for datasets with varying densities or irregularly shaped clusters.
• Robust to Noise and Outliers: The algorithm can handle noise and outliers effectively by designating them as unassigned data points rather than forcing them into a cluster.
• Flexibility in Cluster Shape and Size: Density-based clustering can detect clusters of arbitrary shape and size, allowing for more flexible and nuanced cluster identification.

However, density-based clustering also has some limitations:

• Sensitivity to Parameter Settings: The performance and clustering results of density-based algorithms can be sensitive to the choice of the epsilon radius and minimum number of neighbors.
• Difficulty with High-Dimensional Data: Density-based clustering can be less effective in high-dimensional spaces due to the sparsity of data points in high-dimensional feature spaces.
• Computationally Expensive: The time complexity of density-based clustering algorithms can be relatively high, especially for large datasets.

Density-based clustering finds applications in various fields, including spatial data analysis, image segmentation, anomaly detection, and network analysis. It can help identify hotspots in crime data, segment images based on color similarity, detect outliers in sensor data, or discover communities in social networks.

In summary, density-based clustering algorithms, such as DBSCAN, offer a valuable approach to discovering clusters based on the density of data points. They provide flexibility in handling varying densities, complex cluster shapes, and unknown cluster numbers, making them suitable for a wide range of clustering tasks.

Evaluating Clustering Performance

Evaluating the performance of clustering algorithms is essential to assess the quality of the clustering results and make informed decisions. While clustering is an unsupervised learning task, meaning there are no pre-defined labels for comparison, there are several evaluation metrics and techniques that can be used to evaluate clustering performance. Here are some commonly used methods:

1. Internal Evaluation Metrics: Internal evaluation metrics assess the quality of the clustering results based on the data itself. These metrics measure factors such as compactness, separation, and cohesion of the clusters. Examples include the Silhouette score, Davies-Bouldin index, and Calinski-Harabasz index. Higher values indicate better clustering performance.
2. External Evaluation Metrics: External evaluation metrics compare the clustering results to external reference information, such as pre-existing class labels or ground truth. These metrics evaluate how well the clusters align with the true class labels. Examples include Rand Index, Fowlkes-Mallows Index, and Jaccard Index. Higher values indicate better agreement with the reference labels.
3. Visualization: Visualization techniques can be used to visually examine the clustering results and assess their quality. Scatter plots, heatmaps, and dendrograms can help identify well-separated and distinct clusters, understand the cluster structure, and detect any potential outliers or misclassifications.
4. Cluster Stability: Cluster stability measures the consistency of the clustering results when the algorithm is applied multiple times on slightly perturbed versions of the data. It assesses the robustness of the clustering algorithm and can be useful in choosing the optimal algorithm and parameter settings.
5. Domain-Specific Evaluation: Depending on the specific application, domain-specific evaluation criteria can be used to evaluate clustering performance. For example, in customer segmentation, metrics such as customer lifetime value or conversion rates can be used to assess the effectiveness of the obtained customer segments.

It is important to note that the choice of evaluation metrics depends on the specific characteristics of the dataset, the goals of the clustering task, and the available reference information. Different evaluation metrics may prioritize different aspects of clustering quality, so it is recommended to use multiple metrics for a comprehensive assessment.

Additionally, it is crucial to understand the limitations of evaluation metrics, as no single metric can capture all aspects of clustering performance. Evaluation results should be interpreted alongside domain knowledge and other considerations specific to the application.

In summary, evaluating clustering performance involves assessing the quality of the clustering results using a combination of internal and external evaluation metrics, visualization techniques, cluster stability analysis, and domain-specific evaluation criteria. These evaluation methods provide insights into the effectiveness and reliability of clustering algorithms, helping to make informed decisions and interpretations of the clustering results.

Applications of Clustering in Machine Learning

Clustering, as a fundamental technique in machine learning, finds a wide range of applications across various domains. Let’s explore some of the key applications where clustering plays a vital role:

1. Customer Segmentation: Clustering is extensively used in market research and customer analysis to segment customers based on their preferences, behaviors, or demographics. By identifying distinct customer segments, businesses can tailor their marketing strategies, personalize product offerings, and improve customer satisfaction.
2. Image Recognition and Object Detection: Clustering is crucial in image recognition and object detection tasks. By clustering similar images based on visual features, such as color, shape, and texture, algorithms can group together images showing similar objects or scenes. This aids in tasks such as image retrieval, content-based image searching, and object recognition.
3. Anomaly Detection: Clustering is effective in identifying anomalies or outliers in datasets. By clustering the majority of normal data points together, clusters containing only a few or no data points can be identified as potential anomalies. This is valuable for detecting fraudulent activities, network intrusions, or other unusual behaviors in various domains.
4. Document Clustering and Text Mining: Clustering is widely used in text mining and document analysis to group similar documents together based on their content or themes. It enables tasks such as topic modeling, document organization, sentiment analysis, and document recommendation systems.
5. Market Basket Analysis: Clustering is applied in market basket analysis to identify patterns and associations between products based on customers’ purchase behavior. By clustering products that are frequently purchased together, businesses can uncover interesting insights, such as recommendations for cross-selling and up-selling strategies.
6. Social Network Analysis: Clustering is utilized to analyze and understand social networks by identifying communities or groups within the network. Clustering allows for the discovery of individuals or entities with similar characteristics, aiding in tasks such as targeted advertising, influence analysis, and recommendation systems.
7. Pattern Recognition: Clustering is valuable in pattern recognition tasks, such as speech recognition or handwriting recognition. By clustering similar patterns or patterns belonging to the same class, algorithms can learn to recognize and classify new patterns or objects based on their features.

These are just a few examples of the diverse applications of clustering in machine learning. Clustering contributes to unlocking valuable insights, discovering underlying patterns, and aiding decision-making processes in numerous domains. Its versatility and effectiveness make it an indispensable tool in the field of machine learning.

Conclusion

Clustering is a fundamental technique in machine learning that plays a crucial role in uncovering patterns, generating insights, and aiding decision-making processes. By grouping similar objects or data points together based on their attributes, clustering enables us to identify hidden structures, discover anomalies, segment customers, recommend products, and explore data in a meaningful way.

We explored various aspects of clustering, including its definition, importance in machine learning, common clustering algorithms such as K-means, hierarchical clustering, and density-based clustering. Each algorithm has its strengths and limitations, making them suitable for different types of datasets and applications. We also discussed the evaluation of clustering performance, including internal and external evaluation metrics, visualization techniques, cluster stability, and domain-specific evaluation criteria.

Furthermore, we examined the applications of clustering in machine learning, ranging from customer segmentation and image recognition to anomaly detection and social network analysis. Clustering proves to be a versatile and invaluable technique across a wide range of domains, providing insights, enhancing decision-making, and driving innovation.

As machine learning and data analysis continue to advance, clustering will undoubtedly remain a key pillar in the quest to understand and leverage the vast amounts of data available to us. It provides a powerful approach to organizing, exploring, and extracting valuable knowledge from complex datasets.

With the ever-growing importance of data-driven decision-making, understanding and utilizing clustering techniques will empower us to unlock hidden patterns, gain actionable insights, and make informed choices in a wide range of industries and applications.