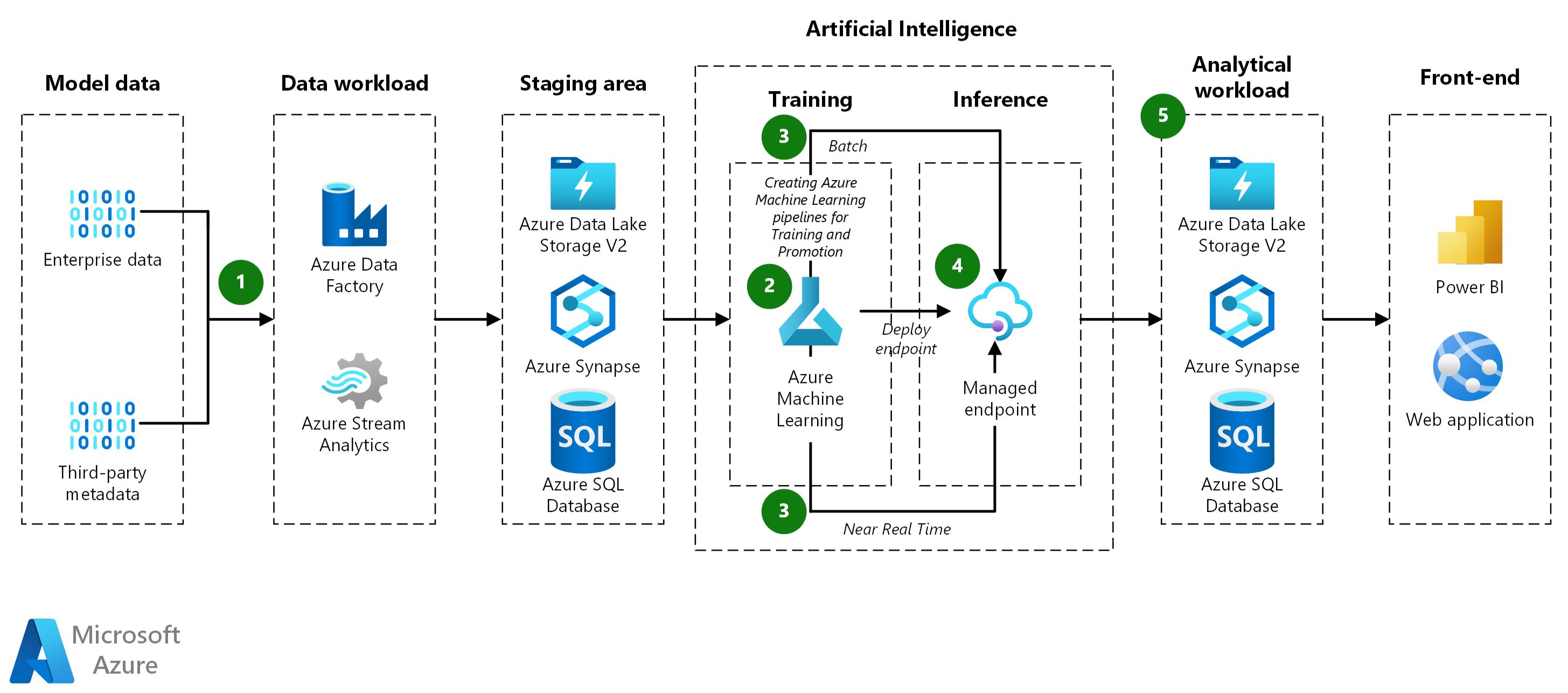
Introduction
Welcome to the world of machine learning, where data is the fuel that powers intelligent algorithms. In the realm of machine learning, the quality and characteristics of the data play a crucial role in the performance and accuracy of the models. One important aspect of data preprocessing is scaling, which involves transforming numerical variables to a common scale. Scaling data is a fundamental step in the preprocessing pipeline and is often used interchangeably with terms like normalization or standardization.
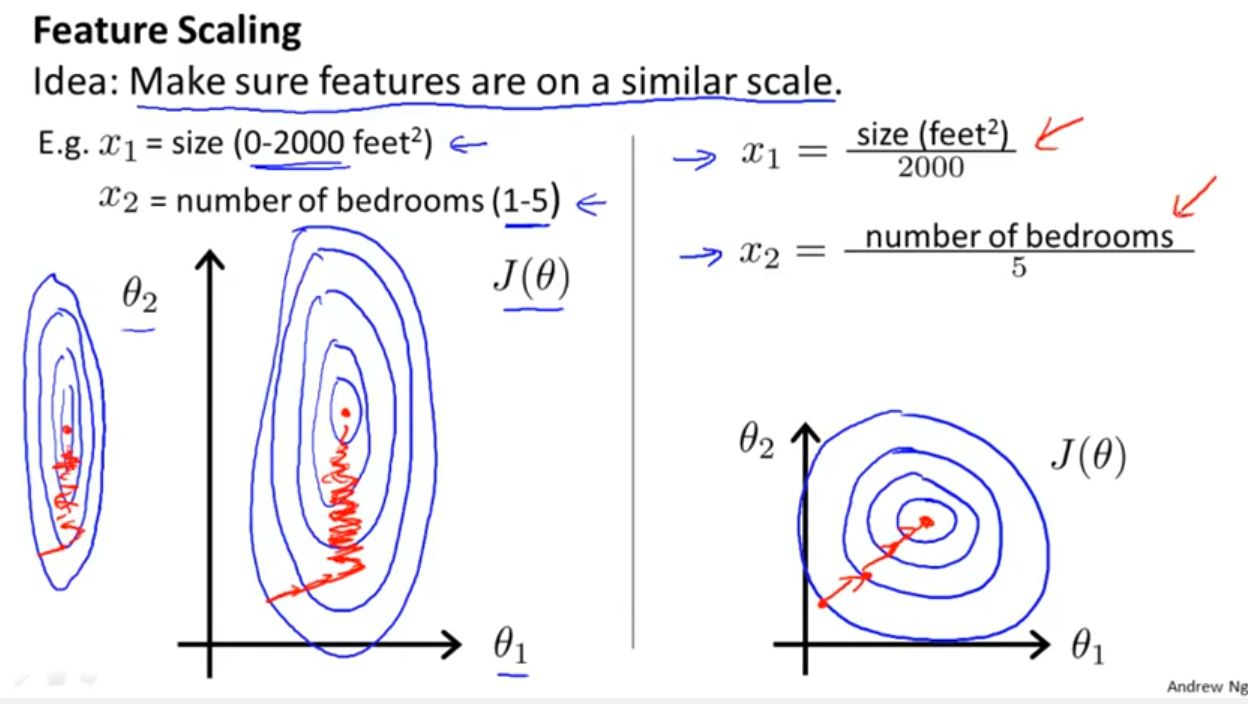
Scaling data is particularly important when dealing with features that have different scales or units of measurement. If the features in the dataset have vastly different ranges, it can negatively impact the learning algorithm’s ability to extract meaningful patterns and relationships. For example, consider a dataset with features like age, income, and number of bedrooms in a house. Age might range from 0 to 100, income from $10,000 to $1,000,000, and number of bedrooms from 1 to 5. Without scaling, the model may give undue importance to income due to its larger range, leading to biased results.
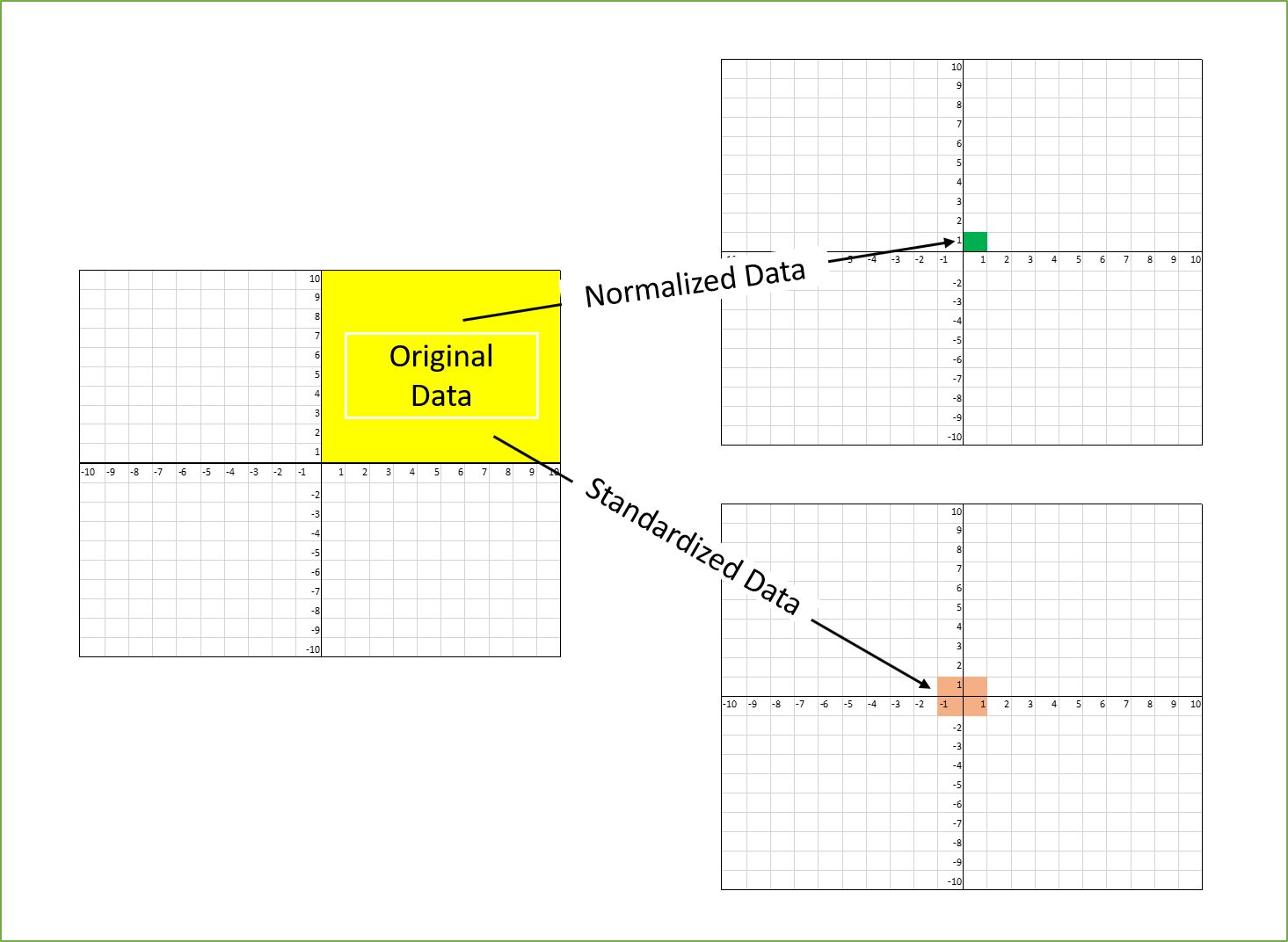
There are different methods to scale data, the two most common being standardization and normalization. Standardization rescales the data to have zero mean and unit variance, whereas normalization rescales the data to a specific range, usually between 0 and 1. The choice of scaling method depends on the specific requirements of the dataset and the machine learning algorithm being used.
In this article, we will discuss the reasons why scaling of data is important in machine learning. We will explore how scaling data ensures fairness in feature comparison, aids in understanding feature importance and interpretability, improves model performance, and reduces computational complexity. By understanding the importance of scaling data, you will be able to make informed decisions about preprocessing your data and improve the accuracy and reliability of your machine learning models.
Standardization
Standardization, also known as z-score normalization, is a common method used to scale data in machine learning. The aim of standardization is to transform the data in such a way that it has zero mean and unit variance. By standardizing the data, each feature will have a similar range and distribution, making it easier for the machine learning algorithm to compare and process the features.
The process of standardization involves subtracting the mean of the feature from each data point and then dividing it by the standard deviation. Mathematically, the standardized value of a data point x can be calculated using the formula:
z = (x – mean) / standard deviation
Standardization is particularly useful when the features in the dataset have significantly different scales or units of measurement. It ensures that no single feature dominates the learning process solely based on its scale. For example, consider a dataset with features like height, weight, and age. The height might range from 150 cm to 190 cm, weight from 50 kg to 100 kg, and age from 20 years to 40 years. Without standardization, the machine learning algorithm might give more importance to weight due to its larger numerical values, leading to biased results.
Standardization also helps in dealing with outliers in the dataset. Outliers are extreme values that deviate significantly from the typical range of values in a dataset. These outliers can have a disproportionate impact on the learning process, especially when using algorithms that are sensitive to the scale of the features. By standardizing the data, the effect of outliers is reduced, making the model more robust to their influence.
Another benefit of standardization is that it makes the interpretation of model parameters easier. When the features are standardized, the model coefficients represent the change in the target variable per unit change in the standardized feature. This makes it easier to compare the importance of different features and interpret their impact on the outcome.
In summary, standardization is a valuable technique for scaling data in machine learning. It ensures that the features are on a similar scale, making it easier for the model to compare and process the data. Standardization also helps in dealing with outliers and facilitates the interpretation of model parameters. By standardizing the data, you can enhance the accuracy and reliability of your machine learning models.
Normalization
Normalization is another commonly used method for scaling data in machine learning. Unlike standardization, which rescales the data to have zero mean and unit variance, normalization transforms the data to a specific range, usually between 0 and 1. This normalization process makes the features comparable and ensures that they fall within a similar numerical range.
There are different types of normalization techniques, including min-max normalization, decimal scaling, and z-score normalization. The most widely used method is min-max normalization, which linearly rescales the data to a specified range. The formula for min-max normalization is:
x_normalized = (x – min) / (max – min)
Here, x is the original data point, min is the minimum value of the feature, and max is the maximum value of the feature. The resulting normalized value lies between 0 and 1, with 0 representing the minimum value and 1 representing the maximum value.
Normalization is particularly useful when the absolute values or the range of the features are not as important as their relative positions or proportions. For example, in image processing, pixel intensities are often normalized to a range of 0 to 1 to ensure consistency and comparability. In recommender systems, user ratings may be normalized to a range of 0 to 1 to facilitate similarity calculations.
Normalization also helps in handling skewed distributions or outliers in the data. By rescaling the data to a specific range, normalization reduces the impact of outliers and ensures that the distribution is not skewed by extremely large or small values. This improves the robustness of the learning algorithm and prevents it from being overly influenced by extreme data points.
Additionally, normalization aids in understanding the relative importance of different features in the dataset. When the features are normalized, their values represent their proportions or ratios within the given range. This allows you to easily compare and evaluate the impact of each feature on the model’s output.
To summarize, normalization is a valuable technique for scaling data in machine learning. It rescales the features to a specific range, making them comparable and ensuring consistency. Normalization also helps in handling skewed distributions and outliers, and enables a meaningful interpretation of feature importance. By applying normalization to your data, you can enhance the performance and reliability of your machine learning models.
Reasons to Scale Data
Scaling the data is an essential step in the preprocessing pipeline of machine learning. Let’s explore some of the key reasons why scaling data is important:
1. Ensuring Fairness: When the features in the dataset have different scales or units of measurement, comparing them becomes challenging. Scaling the data allows for fair and unbiased comparisons between the features, as it brings them to a similar numerical range. This fairness is crucial for the learning algorithm to make accurate and meaningful decisions based on the features.
2. Feature Importance and Interpretability: Scaling data helps in understanding the relative importance of different features. Features with larger numerical values may appear more significant to the machine learning algorithm, leading to biased results. By scaling the data, the features are placed on a similar scale, allowing for a fair evaluation of their impact on the model’s output. This facilitates the interpretation and understanding of feature importance, enabling better decision-making.
3. Improved Model Performance: Scaling the data can significantly enhance the performance of machine learning models. Algorithms like linear regression, support vector machines, and k-nearest neighbors are sensitive to the scale of the features. If the features have different scales, it can negatively impact the model’s ability to extract meaningful patterns and relationships from the data. By scaling the data, the model can learn from the features more effectively, resulting in improved accuracy and predictive performance.
4. Reducing Computational Complexity: Scaling the data can lead to reduced computational complexity, especially in algorithms that involve distance calculations or gradient-based optimization. When features have different scales, the computation of distances or gradients becomes more computationally intensive. Scaling the data ensures that the algorithm operates on features with similar scales, leading to faster and more efficient computations.
By scaling the data, you ensure fairness, improve interpretability, enhance model performance, and reduce computational complexity. These reasons highlight the importance of scaling data in machine learning and emphasize its role in improving the accuracy and reliability of the learning process.
Ensuring Fairness
One of the key reasons to scale data in machine learning is to ensure fairness in the comparison of features. When the features have different scales or units of measurement, it becomes challenging to make meaningful and unbiased comparisons. Scaling the data brings all the features to a similar numerical range, promoting fair evaluations and preventing any one feature from dominating the learning process solely based on its scale.
Consider a practical example of predicting housing prices. The dataset might contain features such as square footage, number of bedrooms, and distance to the nearest school. Square footage values could range from a few hundred to several thousand, while the number of bedrooms could range from one to six. Without scaling, the machine learning algorithm might wrongly assign higher importance to square footage simply due to its larger numeric range, resulting in biased predictions.
Scaling the data resolves this issue by ensuring that all the features have the same scale. This allows for fair comparisons where each feature can be considered on its own merits. By bringing the features to a similar scale, scaling ensures that the model can make accurate and meaningful decisions based on the underlying characteristics of the data rather than the numerical ranges.
Furthermore, scaling data also helps to mitigate the impact of outliers. Outliers are extreme values that deviate significantly from the typical range of values in a dataset. These outliers can skew the learning process and introduce bias. By scaling the data, the effect of outliers is minimized, making the model more robust to their influence. This helps to ensure fairness in the predictions by reducing the undue impact of extreme values.
Scaling the data also contributes to feature fairness by providing a consistent basis for evaluating their importance. When features have different scales, it becomes challenging to compare their relative importance. By scaling the data, the model’s coefficients represent the change in the target variable per unit change in the standardized or normalized feature. This enables a fair and meaningful comparison of feature importance, allowing for better insights into the underlying relationships between features and the target variable.
In summary, ensuring fairness in the comparison of features is a crucial motivation for scaling data in machine learning. Scaling brings all the features to a similar numerical range, allowing for unbiased evaluations and preventing any one feature from dominating the learning process based solely on its scale. By ensuring fairness, scaling data enhances the accuracy and reliability of machine learning models.
Feature Importance and Interpretability
When it comes to machine learning, understanding the relative importance of different features in the dataset is essential for making informed decisions and extracting meaningful insights. Scaling data plays a significant role in assessing feature importance and facilitating interpretability, allowing for better understanding and utilization of the learned models.
When features have different scales or units of measurement, it becomes challenging to compare their importance directly. Scaling the data brings the features to a similar scale, enabling a fair evaluation of their impact on the model’s output. This allows for a more accurate assessment of the relative importance of different features and helps avoid biased results due to numerical disparities.
Additionally, scaling the data helps in interpreting the impact of each feature on the target variable. When features are scaled, the model’s coefficients represent the change in the target variable per unit change in the standardized or normalized feature. This allows for a direct and meaningful interpretation of how each feature influences the model’s predictions.
For example, consider a dataset for predicting car prices, including features like mileage, horsepower, and age. Without scaling, the model might assign more importance to horsepower due to its larger numeric values. However, after scaling the data, the coefficients of the features provide a fair comparison of their actual impact on the predicted car prices. This not only helps in understanding the significance of each feature but also aids in making informed decisions based on their relative importance.
Scaling the data also enhances interpretability by ensuring that the feature’s magnitude is aligned with its importance. In other words, the magnitude of the feature’s coefficient represents the actual magnitude of its impact on the model’s predictions. This helps in building trust in the model and provides insights into how changing the value of a particular feature affects the predicted outcomes.
Furthermore, scaling data also enables visualizations that are more interpretable and meaningful. When features are on a similar scale, visualizing the relationships between features and the target variable becomes more accessible and intuitive. By providing a consistent basis for analysis, scaling helps in extracting insightful patterns and understanding the behavior of the features in relation to the target variable.
In summary, scaling data is crucial for assessing feature importance and facilitating interpretability in machine learning. It allows for unbiased comparisons of feature importance and helps in understanding the impact of each feature on the model’s predictions. By scaling the data, you can improve the interpretability of your models and gain valuable insights into the relationships between features and the target variable.
Improved Model Performance
Scaling the data is a key factor in improving the performance of machine learning models. When features have different scales or units of measurement, it can negatively impact the learning algorithm’s ability to extract meaningful patterns and relationships from the data. Scaling the data addresses this issue by bringing all the features to a similar numerical range, enhancing the model’s performance and accuracy.
Many machine learning algorithms are sensitive to the scale of the features. For example, algorithms like linear regression, support vector machines, and k-nearest neighbors make use of distance-based calculations or optimization methods that require the features to be on a similar scale. If the features have different scales, it can lead to biased results and unreliable predictions.
By scaling the data, these algorithms can learn more effectively from the features. Scaling ensures that the feature values are within a comparable range, allowing the algorithms to accurately assess the impact and relationships between the features and the target variable. This leads to improved model performance by reducing the influence of features with larger scales and enabling more effective feature selection and decision-making.
In addition to improving the performance of machine learning models, scaling the data also facilitates the convergence of optimization algorithms. Gradient-based optimization algorithms, such as those used in neural networks and logistic regression, work more efficiently when the features are on a similar scale. Scaling the data helps to achieve this, ensuring faster convergence and reducing the likelihood of getting stuck in suboptimal solutions.
Furthermore, scaling the data can help to overcome issues related to feature weighting and feature dominance. Features with larger scales may carry more weight in the learning algorithm’s decision-making process. This can lead to biased predictions, as features with smaller scales may be overshadowed and their contributions undervalued. By scaling the data, the algorithm is able to evaluate the features more equitably and give each feature the opportunity to contribute to the model’s predictions in a balanced manner.
Overall, scaling the data significantly enhances the performance of machine learning models by ensuring fair feature evaluation, improving optimization convergence, and preventing feature dominance. By bringing the features to a similar numerical range, scaling enables more accurate predictions and more reliable insights from the models.
Reducing Computational Complexity
Scaling the data not only improves the performance of machine learning models but also reduces computational complexity. In algorithms that involve distance calculations or gradient-based optimization, the scale of the features can significantly impact the computational efficiency of the learning process. By scaling the data, the computational complexity can be reduced, leading to faster and more efficient computations.
When features have different scales, distance-based algorithms, such as k-nearest neighbors and hierarchical clustering, can be affected. In these algorithms, the distance between data points is a critical factor in determining their similarity or dissimilarity. If the features have different scales, the distances calculated may be skewed and not accurately reflect the true underlying patterns in the data. By scaling the data, the algorithm operates on features with similar scales, ensuring that the distances calculated are more representative and meaningful.
Gradient-based optimization algorithms, such as those used in neural networks and logistic regression, are sensitive to the scale of the features. If the features have different scales, the gradient steps taken during the optimization process may vary significantly, leading to slower convergence or convergence to suboptimal solutions. Scaling the data mitigates this issue by bringing the features to a similar scale, allowing for more efficient and effective optimization.
Reducing computational complexity through scaling the data has practical benefits as well. By reducing the computational demands of the learning algorithm, you can perform faster model training and inference, enabling quicker decision-making and enabling real-time applications. This is particularly important when working with large datasets or in resource-constrained environments where computational efficiency is crucial.
In addition, reducing computational complexity can also lead to cost savings. By optimizing the computational resources required for training and inference, you can reduce the time and energy required for processing, lowering the overall computational costs associated with running machine learning algorithms.
Overall, scaling the data plays a vital role in reducing computational complexity in machine learning. By bringing the features to a similar scale, algorithms that involve distance calculations or gradient-based optimization can operate more efficiently and effectively. This reduction in computational complexity leads to faster computations, improved convergence, cost savings, and enables real-time and resource-efficient machine learning applications.
Conclusion
Scaling data is a crucial step in the preprocessing pipeline of machine learning, as it has a significant impact on the performance, fairness, interpretability, and computational efficiency of the models. Through techniques like standardization and normalization, scaling helps to bring features to a similar numerical range, ensuring fair comparisons, facilitating the interpretation of feature importance, improving model performance, and reducing computational complexity.
By scaling the data, the model can make unbiased and accurate evaluations of the features, preventing any one feature from dominating the learning process solely based on its scale. Scaling also enables a fair comparison of feature importance, allowing for a better understanding of their individual contributions to the model’s predictions. It enhances interpretability by ensuring that the magnitude of the features aligns with their importance, making it easier to interpret the impact of each feature on the target variable.
Furthermore, scaling the data significantly improves model performance by enabling algorithms to learn more effectively from the features. It allows the models to extract meaningful patterns and relationships by reducing the influence of features with larger scales and enhancing feature selection and decision-making processes.
In addition to performance improvements, scaling data also reduces computational complexity. By bringing features to a similar scale, distance-based algorithms and gradient-based optimization algorithms can operate more efficiently and accurately. This leads to faster model training, quicker decision-making, cost savings, and enables real-time and resource-efficient machine learning applications.
In summary, scaling data in machine learning is critical for achieving reliable and accurate results. It encompasses various techniques and considerations that ensure fairness, interpretability, improved performance, and reduced computational complexity. By understanding the importance of scaling data and applying appropriate scaling techniques, you can enhance the accuracy, reliability, and feasibility of your machine learning models.