Introduction
Welcome to the world of machine learning, where algorithms and models are driving revolutionary advancements in various fields. Among these powerful algorithms, lasso regression stands out as an important technique for solving regression problems. In this article, we will explore what lasso regression is, how it works, its differences from ridge regression, and its benefits and drawbacks.
Regression analysis is a fundamental concept in machine learning and statistics. It involves predicting a continuous numerical output based on a set of input variables. Lasso regression, also known as L1 regularization, is a type of linear regression that combines both feature selection and regularization to improve the accuracy and interpretability of the model.
Unlike traditional linear regression, which often includes all available features in the model, lasso regression performs automatic feature selection by shrinking the coefficients of less relevant variables towards zero. This property is particularly useful in situations where there are many input variables, and we want to identify the most important ones.
Lasso regression achieves feature selection by introducing an additional penalty term to the loss function. This penalty term is the sum of the absolute values of the coefficients, multiplied by a hyperparameter called the regularization parameter. By adjusting this regularization parameter, we can control the amount of shrinkage applied to the coefficients.
The beauty of lasso regression lies in its ability to effectively eliminate irrelevant features from the model, leaving only the most important ones. This not only improves the model’s accuracy by reducing overfitting, but also enhances its interpretability by highlighting the influential factors driving the predictions.
In the next section, we will dive deeper into how lasso regression works and how it differs from ridge regression.
What is Lasso Regression?
Lasso regression, short for Least Absolute Shrinkage and Selection Operator, is a technique used in machine learning and statistics for regression analysis. It is an extension of linear regression that adds a regularization term to the loss function, resulting in improved model performance and feature selection.
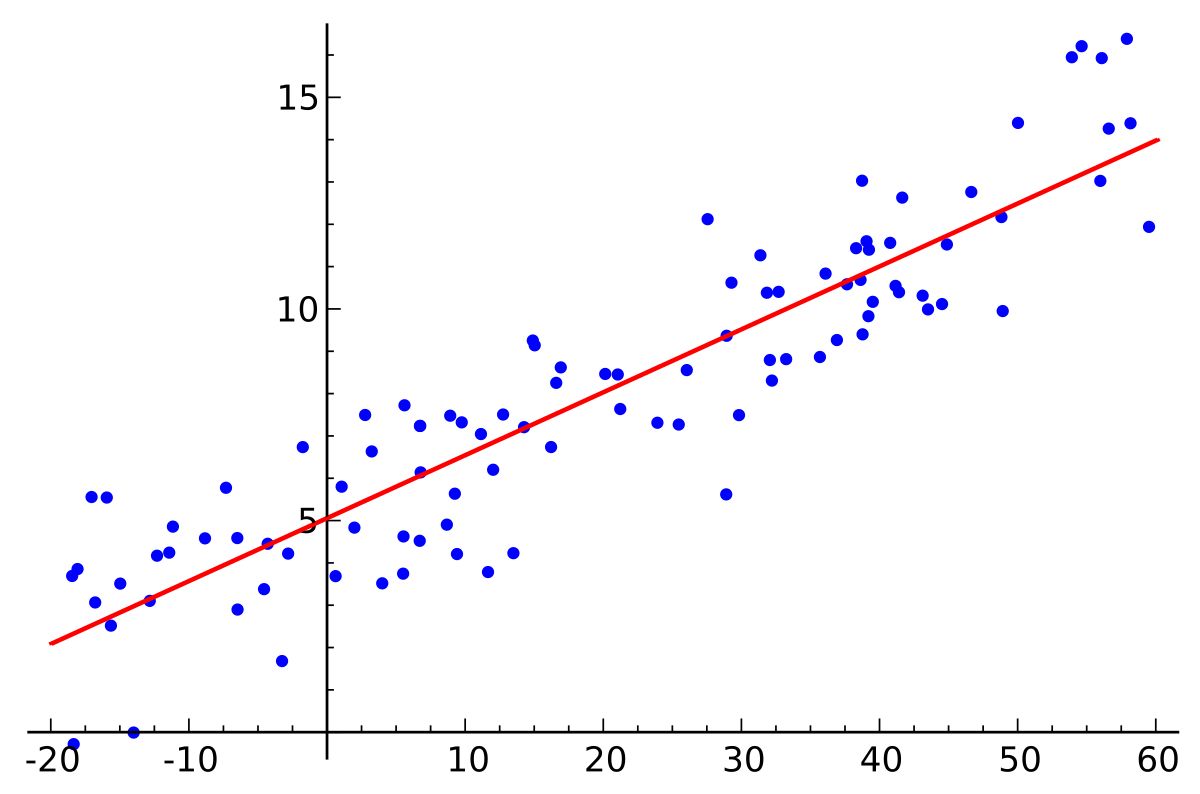
In traditional linear regression, the goal is to minimize the sum of squared residuals between the predicted and actual values. This method works well when the number of features is small and there is little to no multicollinearity among them. However, in the presence of multiple correlated features, linear regression may lead to overfitting and unstable coefficient estimates.
Lasso regression addresses these issues by adding a penalty term to the loss function. This penalty term is the sum of the absolute values of the coefficients multiplied by a hyperparameter called the regularization parameter or lambda. The lambda value determines the amount of shrinkage applied to the coefficients.
The main advantage of lasso regression is its ability to perform feature selection. By shrinking the coefficients of less important variables to zero, lasso regression effectively disregards those features in the final model. This makes it particularly useful when dealing with datasets that contain a large number of input variables, as it helps to identify the most relevant features and simplify the model.
Compared to other regularization techniques such as ridge regression, which uses the squared values of the coefficients as the penalty term, lasso regression tends to produce sparse solutions. This means that it promotes sparsity in the coefficient estimates, leading to models with fewer non-zero coefficients. This property makes the model easier to interpret and can help uncover the important predictors that drive the output variable.
To summarize, lasso regression is a powerful technique that combines feature selection and regularization to improve the performance and interpretability of regression models. By adding a penalty term to the loss function, lasso regression encourages sparsity and automatically selects the most relevant features for the final model. In the next section, we will explore how lasso regression works in more detail and compare it to ridge regression.
How Does Lasso Regression Work?
Lasso regression works by introducing a penalty term into the loss function of linear regression. This penalty term, also known as L1 regularization, encourages the coefficient values of less important features to be shrunk towards zero, effectively performing feature selection.
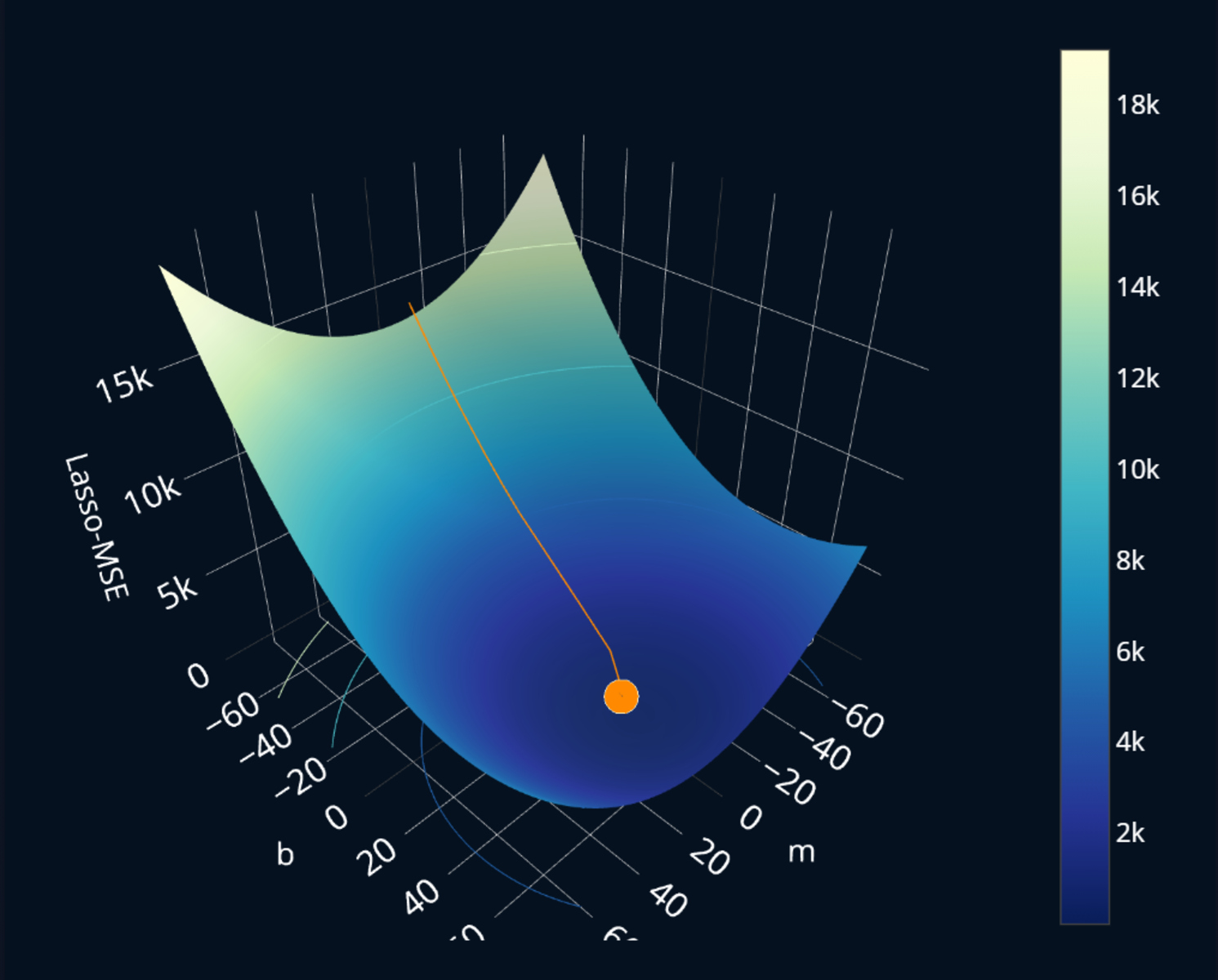
The core idea behind lasso regression is to find the set of coefficient values that minimize the loss function, subject to the constraint that the sum of the absolute values of the coefficients is less than or equal to a specified constant. Mathematically, this can be represented as:
Minimize: Loss function + λ * Sum of absolute values of coefficients
Here, λ represents the regularization parameter, which controls the amount of shrinkage applied to the coefficients. A higher λ value will result in more coefficient shrinkage and more sparsity in the model, while a lower λ value will allow the coefficients to take higher absolute values.
The lasso regression algorithm iteratively adjusts the coefficients to minimize the loss function and the penalty term. At each iteration, the algorithm assesses the impact of each feature and decides whether to include it in the model or set its coefficient to zero. If the feature is deemed significant, its coefficient is non-zero; otherwise, it is set to zero.
One important characteristic of lasso regression is that it can generate sparse solutions. This means that many of the coefficients in the final model will be exactly zero, indicating that the corresponding features are not considered relevant. By effectively eliminating irrelevant features, lasso regression simplifies the model and improves interpretability.
In addition to its feature selection capabilities, lasso regression also serves as a regularization technique. By shrinking the coefficients towards zero, lasso regression helps reduce the risk of overfitting. Overfitting occurs when the model captures noise and random fluctuations in the training data, leading to poor generalization performance on unseen data. Lasso regression’s regularization helps prevent overfitting by discouraging the model from relying too heavily on any single feature.
It’s important to note that the performance of lasso regression can be influenced by the choice of the regularization parameter, λ. A higher λ value will produce a more parsimonious model but may discard important features, while a lower λ value may keep more features but increase the risk of overfitting. Cross-validation techniques can be used to identify the optimal λ value that balances model complexity and predictive accuracy.
In the next section, we will compare lasso regression to another popular regularization technique, ridge regression, and explore their differences and use cases.
Lasso Regression vs. Ridge Regression
Lasso regression and ridge regression are both popular regularization techniques used in linear regression models. While they share similarities, they differ in how they penalize the coefficients and handle feature selection.
The key distinction between lasso regression and ridge regression lies in the penalty term used in their loss functions. Lasso regression uses L1 regularization, which adds the sum of the absolute values of the coefficients multiplied by a regularization parameter (λ) to the loss function. In contrast, ridge regression uses L2 regularization, which adds the sum of the squared values of the coefficients multiplied by the regularization parameter to the loss function.
This difference in the penalty term leads to different effects on the model. Lasso regression has the capacity to set some coefficient values exactly to zero, effectively performing feature selection. This sparsity-inducing property makes lasso regression beneficial when dealing with datasets that have many input variables and when identifying the most important features is crucial. On the other hand, ridge regression includes all features in the model but reduces the magnitude of their coefficients, which helps prevent overfitting.
When it comes to interpretability, lasso regression often provides more understandable results. Since it can eliminate irrelevant features and shrink others to zero, the resulting model includes only the most important variables. This feature selection aspect of lasso regression makes it easier to identify the influential factors driving the predictions. In contrast, ridge regression includes all features in the model, albeit with smaller coefficients, which can make interpretation more challenging.
The choice between lasso regression and ridge regression depends on the specific problem and dataset at hand. Lasso regression is typically favored when feature selection is a priority or when the dataset has many correlated features. It helps simplify the model and identify the most relevant variables. On the other hand, ridge regression is useful when all features are expected to contribute to the output, but their magnitudes need to be constrained to prevent overfitting.
In practice, it is not uncommon to explore both lasso regression and ridge regression and compare their performance. This can be done by tuning the regularization parameters (λ) for both techniques using techniques like cross-validation. It is also possible to combine the benefits of lasso and ridge regression by using an elastic net approach, which adds both L1 and L2 regularization terms to the loss function.
Now that we have explored the differences between lasso regression and ridge regression, let’s look at the benefits and drawbacks of using lasso regression in more detail.
Benefits and Drawbacks of Lasso Regression
Lasso regression offers several benefits and drawbacks that make it a powerful technique for regression analysis. Understanding these pros and cons can help determine when and where to apply lasso regression in machine learning projects.
One of the major benefits of lasso regression is its ability to perform feature selection automatically. By shrinking the coefficients of less important variables towards zero, lasso regression identifies and disregards irrelevant features in the model. This feature selection aspect not only helps improve the model’s accuracy by reducing overfitting but also enhances its interpretability by highlighting the most influential factors driving the predictions. The sparsity-inducing nature of lasso regression makes it particularly useful when dealing with datasets that contain a large number of input variables.
Another advantage of lasso regression is its ability to handle multicollinearity among predictors. When there are multiple variables that are highly correlated with each other, traditional methods like linear regression may produce unreliable coefficient estimates. Lasso regression effectively deals with this issue by shrinking the coefficients towards zero, resulting in more stable and interpretable estimates.
Additionally, lasso regression serves as a regularization technique that helps prevent overfitting. Overfitting occurs when a model captures noise and random fluctuations in the training data, leading to poor generalization performance on unseen data. By introducing a penalty term to the loss function, lasso regression discourages the model from relying too heavily on any single feature, thereby reducing the risk of overfitting and improving the model’s ability to generalize to new data.
Despite its advantages, lasso regression has some limitations and drawbacks. One limitation is its sensitivity to the choice of the regularization parameter, λ. The λ value controls the amount of shrinkage applied to the coefficients, and selecting an appropriate value is crucial. If the λ value is too large, lasso regression may discard important features, resulting in an underperforming model. Conversely, if the λ value is too small, lasso regression may not effectively shrink the coefficients, leading to overfitting.
Another drawback is that lasso regression tends to perform poorly when the dataset contains highly correlated features. In such cases, lasso regression may arbitrarily select one feature over another with little theoretical justification. This can make the results less stable and difficult to interpret.
Furthermore, lasso regression assumes that the relationship between the input variables and the output variable is linear. If the relationship is nonlinear, lasso regression may provide suboptimal results or fail to capture the true underlying pattern in the data. In such cases, alternative techniques that can model nonlinear relationships, such as polynomial regression or tree-based methods, may be more appropriate.
Despite these limitations, lasso regression remains a valuable tool in the arsenal of machine learning practitioners. It offers automatic feature selection, the ability to handle multicollinearity, and regularization to prevent overfitting. By carefully considering the benefits and drawbacks of lasso regression, one can leverage its strengths to build accurate and interpretable regression models.
In the next section, we will see how lasso regression can be implemented in Python by using the scikit-learn library.
Implementation and Example in Python
Lasso regression implementation in Python is made easier by the scikit-learn library, which provides a comprehensive set of tools for machine learning. Let’s walk through an example of how to perform lasso regression using scikit-learn.
First, you need to import the necessary modules:
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
Next, load your dataset and split it into training and testing sets:
# Load the dataset
X, y = load_dataset()
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
Create an instance of the Lasso regression model, specifying the regularization parameter (alpha):
# Create an instance of the Lasso model
lasso = Lasso(alpha=0.1)
Fit the model to the training data:
# Fit the model to the training data
lasso.fit(X_train, y_train)
Make predictions on the testing data:
# Make predictions on the testing data
y_pred = lasso.predict(X_test)
Evaluate the model performance using a suitable metric, such as mean squared error:
# Calculate the mean squared error
mse = mean_squared_error(y_test, y_pred)
Finally, you can analyze the coefficients and identify the important features of the model:
# Get the coefficients
coefficients = lasso.coef_
# Identify the important features
important_features = [feature for feature, coefficient in zip(X.columns, coefficients) if coefficient != 0]
This example demonstrates how to implement lasso regression in Python using scikit-learn. Remember to preprocess your data, handle missing values, and perform any necessary feature engineering before fitting the model. Additionally, it’s essential to tune the regularization parameter (alpha) to find the optimal balance between model complexity and predictive accuracy.
Now that you have an understanding of lasso regression implementation in Python, let’s summarize the key points before concluding our discussion.
Conclusion
In conclusion, lasso regression is a powerful technique for regression analysis that combines feature selection and regularization. It adds a penalty term to the loss function of linear regression, encouraging the coefficients of less important variables to be shrunk towards zero. The sparsity-inducing property of lasso regression makes it highly effective in situations with high-dimensional datasets, where it can automatically select the most relevant features and improve model interpretability.
We have seen that lasso regression offers several benefits, including automatic feature selection, handling of multicollinearity, and regularization to prevent overfitting. By successfully eliminating irrelevant features and shrinkage the coefficients, lasso regression simplifies the model, improves accuracy, and enhances interpretability.
However, lasso regression also has some limitations. It requires careful selection of the regularization parameter, as an inappropriate value may lead to underfitting or overfitting. Additionally, lasso regression performs poorly when dealing with highly correlated features and assumes linearity in the relationships between input and output variables.
Despite these limitations, lasso regression remains a valuable tool in the field of machine learning. Its implementation using Python and libraries like scikit-learn is straightforward, making it accessible to both beginners and experienced practitioners. By tuning the regularization parameter and applying feature engineering techniques, lasso regression can be an effective solution to regression problems.
Whether you need to identify important features, improve model accuracy, or enhance interpretability, lasso regression is a versatile technique that can meet your needs. By leveraging its strengths and considering its limitations, you can unlock the potential of lasso regression in your machine learning projects.
We hope this article has provided you with a comprehensive understanding of lasso regression and its applications. Now, it’s time to apply this knowledge to your own projects and explore the benefits of lasso regression further.