What Is Cosine Similarity In Machine Learning

Introduction

When it comes to machine learning and natural language processing, one of the most commonly used techniques for measuring similarity between textual documents or vectors is cosine similarity. Cosine similarity is a fundamental concept that plays a crucial role in various applications, such as information retrieval, recommendation systems, and clustering algorithms.

Cosine similarity is a mathematical measurement used to determine how similar two vectors are in a multi-dimensional space. It is particularly useful in text analysis tasks, where documents are represented as high-dimensional vectors. By calculating the cosine similarity between these vectors, we can gauge the similarity between the documents, regardless of their length or magnitude.

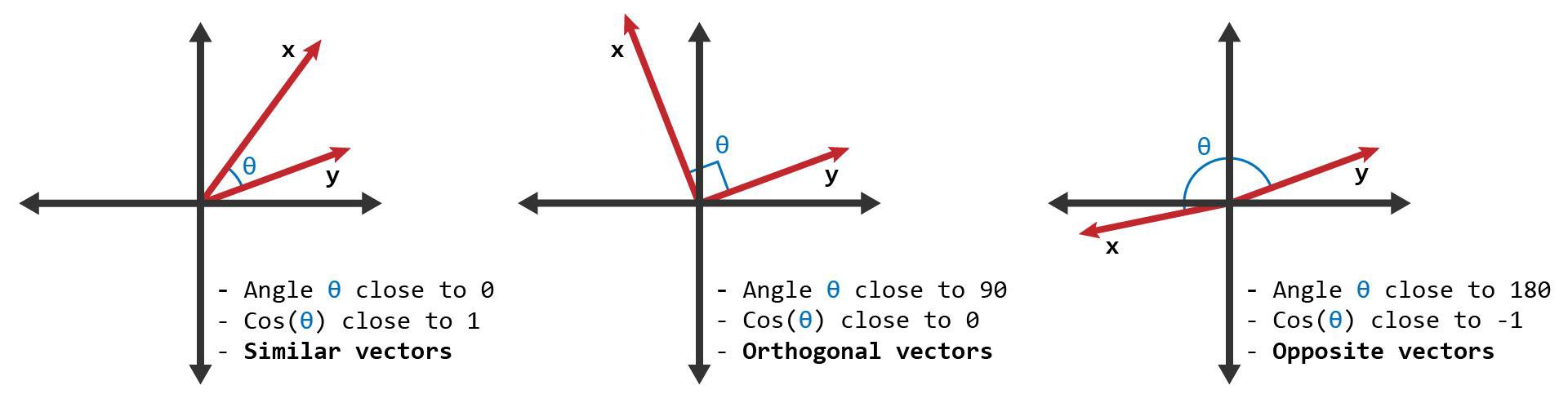
In essence, cosine similarity measures the angle between two vectors, where a smaller angle indicates a higher similarity. The range of cosine similarity lies between -1 and 1, with 1 representing identical vectors, 0 indicating no similarity, and -1 signifying complete dissimilarity.

Understanding cosine similarity is crucial for practitioners in various fields, especially those working with large textual datasets. This metric allows them to quantify relationships between documents and use this information to perform tasks like document clustering, document retrieval, and recommendation systems.

In this article, we will delve into the details of cosine similarity, exploring how it works, how to calculate it, and its application in machine learning. We will also discuss its advantages and limitations that practitioners should be aware of. So, let’s dive in and unravel the fascinating world of cosine similarity.

What is Cosine Similarity?

Cosine similarity is a metric used to determine the similarity between two vectors in a multi-dimensional space. It measures the cosine of the angle between the vectors, hence the name “cosine similarity”. The vectors can represent documents, sentences, or any other data points that can be represented as a set of numerical features.

Unlike some other similarity measures, cosine similarity is not affected by the magnitudes of the vectors or their lengths. This makes it a popular choice in natural language processing tasks, where document lengths can vary significantly. By focusing on the angle between the vectors, cosine similarity captures the directionality of the vectors rather than their absolute values.

In the context of text documents, cosine similarity hinges on the idea that similar documents will have similar distributions of words. By representing documents as vectors, where each dimension represents the frequency or presence of a particular word, cosine similarity can quantify the similarity between two documents based on their word distributions.

Cosine similarity is particularly useful because it provides a value between -1 and 1, where -1 represents complete dissimilarity, 0 denotes no similarity, and 1 signifies identical documents. This allows us to compare documents and understand the degree to which they are similar or dissimilar.

It’s important to note that while cosine similarity is often applied to text analysis tasks, it can also be used in other domains, such as image recognition or recommender systems. In these cases, vectors may represent image features or user preferences, and cosine similarity can aid in measuring the similarity between them.

How Does Cosine Similarity Work?

Cosine similarity calculates the similarity between two vectors by measuring the angle between them in a multi-dimensional space. It determines the cosine of the angle, which ranges between -1 and 1, representing complete dissimilarity and perfect similarity, respectively.

To understand how cosine similarity works, let’s consider two vectors, A and B, represented by their feature values. These feature values can be the frequency of words in a document or any other numerical representation of data points. The cosine similarity is calculated using the dot product of the two vectors and their magnitudes.

The dot product of two vectors A and B is the sum of the products of their corresponding feature values. Mathematically, it is represented as:

Dot Product (A, B) = (A1 * B1) + (A2 * B2) + … + (An * Bn)

The magnitudes of the vectors are calculated as the square root of the sum of the squares of their feature values. Mathematically, the magnitude of a vector A is represented as:

Magnitude (A) = sqrt(A1^2 + A2^2 + … + An^2)

Using the dot product and magnitudes, we can then calculate the cosine similarity between vectors A and B as:

Cosine Similarity (A, B) = Dot Product (A, B) / (Magnitude (A) * Magnitude (B))

By dividing the dot product by the product of the magnitudes, cosine similarity normalizes the similarity measure, making it independent of the vector lengths. This ensures that comparisons between vectors are based solely on their directional similarities, rather than their magnitudes.

Overall, cosine similarity provides a reliable measure of similarity between vectors in a high-dimensional space, making it a valuable tool in various machine learning tasks.

Calculating Cosine Similarity

Calculating cosine similarity involves a straightforward mathematical process that can be performed using various programming languages or libraries. The steps involved are as follows:

1. Create vectors: First, represent the data points you want to compare as vectors. Each element of the vector corresponds to a specific feature or attribute of the data.
2. Normalize vectors: To ensure accurate comparison, it is important to normalize the vectors by dividing each element by the magnitude of the vector. This step is essential to remove any bias introduced by vector length.
3. Calculate dot product: Compute the dot product between the two normalized vectors. This involves multiplying corresponding elements of the vectors and summing the results. The dot product represents the similarity between the vectors.
4. Calculate magnitudes: Calculate the magnitudes of the normalized vectors by taking the square root of the sum of the squared elements. The magnitudes are used to normalize the dot product.
5. Compute cosine similarity: Finally, divide the dot product by the product of the magnitudes to obtain the cosine similarity score. This value will be between -1 and 1, indicating the similarity between the two vectors.

It’s important to note that there are efficient libraries and functions available in most programming languages for calculating cosine similarity. These libraries often provide optimized implementations that can handle large datasets more efficiently.

Additionally, it’s worth mentioning that cosine similarity is just one of many similarity measures available. The choice of similarity measure depends on the specific problem and the nature of the data being analyzed. Other metrics like Euclidean distance or Jaccard similarity may be more suitable in certain scenarios.

By calculating cosine similarity, you can gain valuable insights into the similarity or dissimilarity between vectors, allowing you to make informed decisions in various machine learning and data analysis tasks.

Using Cosine Similarity in Machine Learning

Cosine similarity is widely utilized in machine learning, particularly in tasks that involve comparing and analyzing textual data. Here are some common applications of cosine similarity in machine learning:

• Information retrieval: Cosine similarity is often used in search engines and document retrieval systems. By calculating the similarity between user queries and indexed documents, search engines can provide relevant results based on the cosine similarity scores.
• Text classification: Cosine similarity can be used to classify texts based on their similarity to predefined classes or categories. By comparing the cosine similarity between a document and class prototypes, text classifiers can assign the document to the most similar class.
• Recommendation systems: Cosine similarity plays a crucial role in content-based recommendation systems. By representing user preferences and item features as vectors, cosine similarity can identify items that are most similar to a user’s preferences, enabling personalized recommendations.
• Clustering: Cosine similarity is commonly used in clustering algorithms, such as k-means clustering. By measuring the similarity between data points, the algorithm groups similar points together, allowing for the identification of underlying patterns and structures in the data.

These are just a few examples of how cosine similarity is employed in machine learning. Its versatility and effectiveness make it a valuable tool in a wide range of applications.

Furthermore, cosine similarity can be combined with other techniques to enhance the performance of machine learning models. For instance, it can be used in ensemble methods where multiple similarity measures are combined to improve accuracy.

It’s worth noting that while cosine similarity is commonly associated with textual data, it is not limited to this domain. It can be applied to any data that can be represented as vectors, making it a versatile metric for various machine learning tasks involving similarity measurements.

Advantages of Cosine Similarity

Cosine similarity offers several advantages that make it a popular choice in machine learning and natural language processing tasks. Here are some key advantages of using cosine similarity:

• Robust to document length: Unlike some other similarity measures, cosine similarity is not affected by the length of documents. This is particularly advantageous in text analysis tasks where documents can vary significantly in length. Cosine similarity focuses on the angle between vectors, capturing the directionality of the data rather than its magnitude.
• Multilingual compatibility: Cosine similarity can be applied to texts in different languages without the need for language-specific preprocessing or feature engineering. As long as the texts are represented as vectors, cosine similarity can effectively measure their similarity regardless of the language used.
• Efficient computation: Calculating cosine similarity is a computationally efficient process, especially when dealing with high-dimensional data. The simplicity of the cosine similarity formula allows for fast calculations, making it suitable for real-time or large-scale applications.
• Interpretability: Cosine similarity produces a similarity score that is intuitive to interpret. The range of -1 to 1 provides a clear indication of the degree of similarity between vectors. Values close to 1 indicate high similarity, while values close to -1 indicate dissimilarity.
• Suitable for sparse data: When dealing with sparse data, where most elements are zero, cosine similarity performs well. It only considers non-zero elements, making it robust to the sparsity of the data. This is particularly useful in text analysis tasks where the bag-of-words representation often leads to sparse vectors.

By leveraging these advantages, cosine similarity enables effective similarity measurement, facilitating the development of robust and efficient machine learning models.

Limitations of Cosine Similarity

While cosine similarity is a powerful tool for measuring similarity between vectors, it does have some limitations that should be taken into account. Here are some notable limitations of cosine similarity:

• Insensitive to semantic meaning: Cosine similarity only considers the frequency or presence of words in the vectors and does not take into account the meaning or semantics of the words. Documents with similar word distributions but different meanings may still be assigned high cosine similarity scores.
• Does not capture word order: Cosine similarity treats documents as bags of words, ignoring the order in which the words occur. This can result in loss of important sequential information, especially in tasks where word order is significant, such as sequence classification or sentiment analysis.
• Sensitive to vector representation: The choice of vector representation can greatly impact cosine similarity results. Different techniques for transforming data into vectors, such as TF-IDF or word embeddings, can yield different similarity scores. It is essential to choose a suitable vector representation method that aligns with the task and data at hand.
• Unweighted similarity: Cosine similarity treats all features with equal importance. In certain cases, weighting certain features or dimensions may be more appropriate based on domain knowledge or specific requirements of the problem. In such scenarios, alternative similarity measures that incorporate weights may be more suitable.

It’s essential to be aware of these limitations and consider them when applying cosine similarity in machine learning tasks. Depending on the specific problem and data characteristics, alternative similarity measures that address these limitations, such as modified angular similarity or semantic similarity metrics, may be more appropriate.

Despite its limitations, cosine similarity remains a valuable tool in various applications. By understanding its strengths and weaknesses, practitioners can make informed decisions and leverage cosine similarity effectively in their machine learning pipelines.

Conclusion

Cosine similarity is a fundamental concept in machine learning and natural language processing that allows us to measure the similarity between vectors in a multi-dimensional space. By defining the angle between vectors, cosine similarity provides a robust and efficient method for comparing textual documents, recommending items, clustering data, and more.

In this article, we explored the concept of cosine similarity, its calculation process, and its applications in machine learning. We learned that cosine similarity is particularly advantageous when dealing with documents of varying lengths, as it focuses on the directionality of vectors rather than their magnitudes. Moreover, cosine similarity is language-agnostic and computationally efficient, making it suitable for a wide range of tasks.

However, it’s important to bear in mind the limitations of cosine similarity. It is not sensitive to word semantics or word order, and the choice of vector representation can impact the results. Alternative similarity measures may need to be considered depending on the specific requirements of the task.

Despite its limitations, cosine similarity remains a valuable tool that forms the basis for many machine learning algorithms and applications. By understanding its strengths and weaknesses, practitioners can leverage cosine similarity effectively to gain insights, make recommendations, classify data, and more.

As machine learning continues to advance, cosine similarity will likely evolve alongside it. Researchers and practitioners are constantly exploring new techniques that can enhance its effectiveness and address its limitations. By staying informed and following these developments, we can continue to make use of cosine similarity’s power to unlock meaningful patterns and relationships within data in the future.