What Is Vector In Machine Learning

Introduction

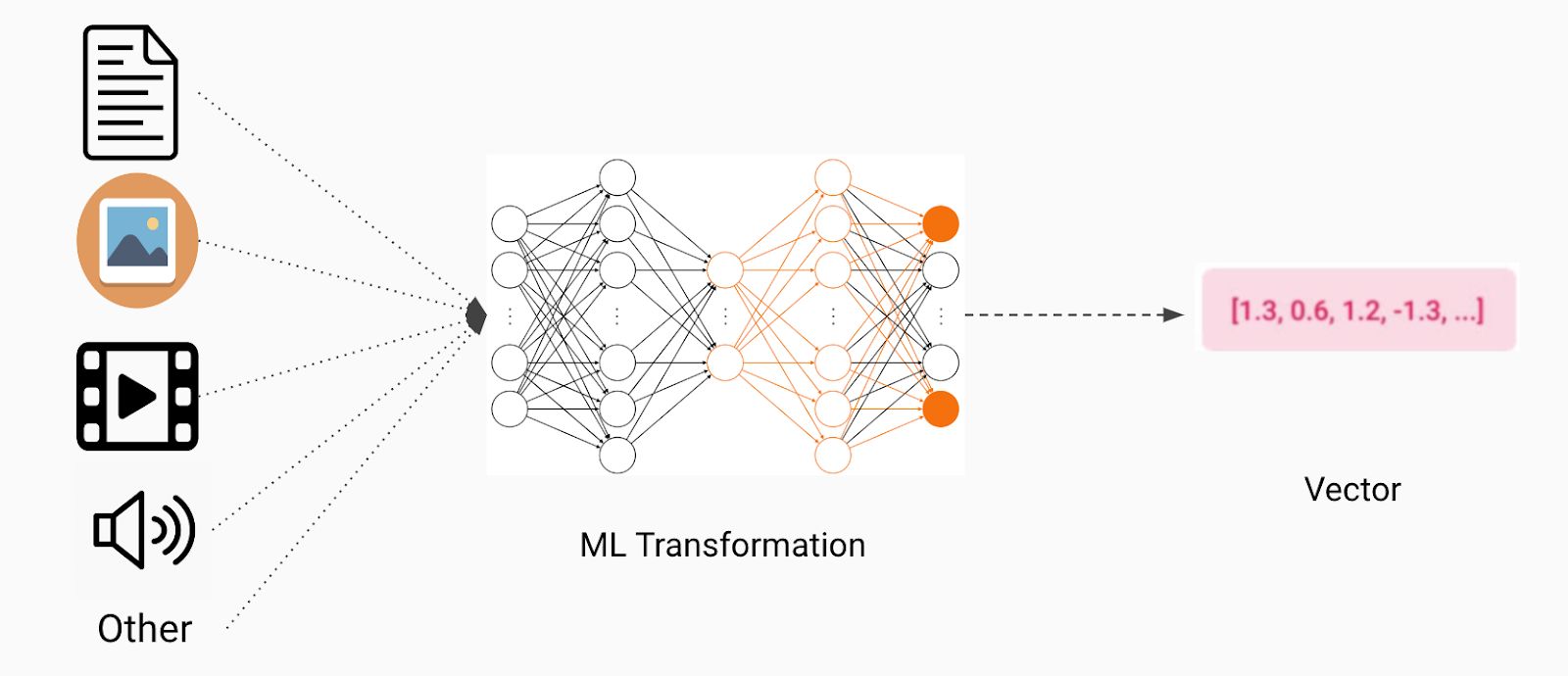
Machine learning is a field of study that focuses on developing algorithms and models that enable computers to learn and make predictions or decisions without being explicitly programmed. One of the fundamental concepts in machine learning is the use of vectors. Vectors play a vital role in representing and processing data in various machine learning tasks, from classification to regression, and much more.

A vector is a mathematical object that represents a quantity with both a magnitude and direction. In the context of machine learning, vectors can be thought of as multidimensional arrays that store numeric values. These values can represent various characteristics or attributes associated with a data point or an observation.

Vectors are extensively used in machine learning due to their ability to compactly represent complex data. They have become an integral part of input and output representations, allowing machines to efficiently process and manipulate data for making informed decisions.

In the following sections, we will delve deeper into the definition of vectors, the different types of vectors used in machine learning, their features, common vector operations, and the applications of vectors in machine learning tasks.

Definition of Vector

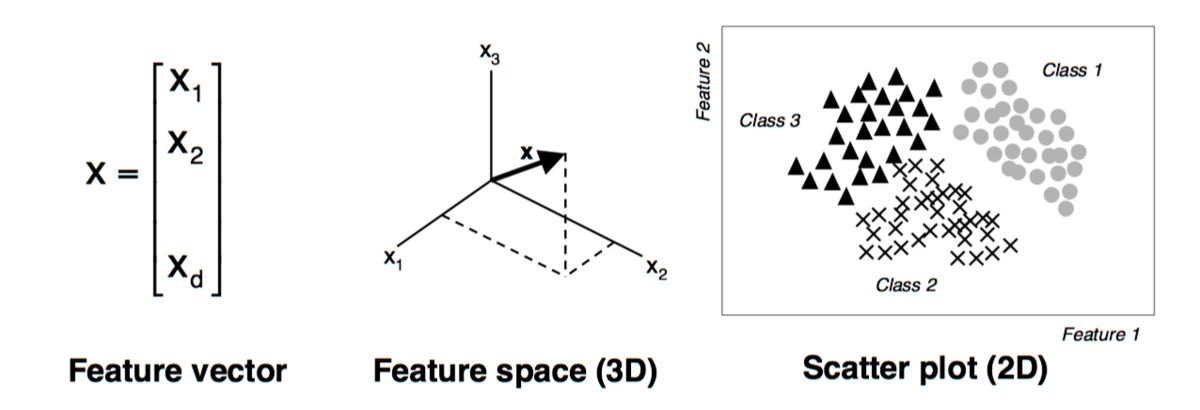
In the context of machine learning, a vector is a mathematical object that represents a data point in a multidimensional space. It consists of a set of numeric values, also known as components or coordinates, that correspond to different attributes or features of the data.

A vector can be represented as an ordered list of elements enclosed within square brackets, such as [x1, x2, x3, …, xn]. Each element in the list corresponds to a specific dimension or attribute of the data point. For example, in a dataset of house prices, a vector could represent a single house with elements for the number of bedrooms, square footage, location, and other relevant features.

The number of elements in a vector is referred to as its dimensionality. A vector with n elements is said to be an n-dimensional vector. For example, a 3-dimensional vector represents a data point in a three-dimensional space, where the coordinates determine the position of the point along each axis.

In machine learning, vectors are often used to represent both input data (features) and output data (labels or targets). Input vectors capture the information or attributes associated with each data point, while output vectors represent the desired predictions or classifications for the corresponding inputs.

Vectors can take on different forms and characteristics depending on the type of data being represented. They can be continuous or discrete, numerical or categorical. Continuous vectors consist of real-valued numbers, while discrete vectors contain integers or other discrete values. Numerical vectors are used to represent quantitative data, while categorical vectors capture qualitative or categorical information.

Overall, vectors in machine learning are an essential tool for organizing, representing, and manipulating data. They provide a way to condense complex information into a structured format that can be efficiently processed by machine learning algorithms.

Types of Vectors in Machine Learning

Vectors in machine learning can take on different forms and serve various purposes depending on the task at hand. Here are some common types of vectors used in machine learning:

1. Input Vectors: These vectors represent the features or attributes of the input data points. Each element in the vector corresponds to a specific feature, such as the pixel values of an image or the numerical values of different measurements. Input vectors provide the necessary information for machine learning algorithms to learn patterns and make predictions.
2. Output Vectors: Output vectors, also known as target vectors, represent the desired predictions or classifications for the input data points. In supervised learning tasks, the output vector contains the correct labels or target values associated with the inputs. For example, in a spam email classification task, the output vector can be [0, 1], where 0 represents a non-spam email and 1 represents a spam email.
3. Binary Vectors: Binary vectors are a type of discrete vector that only contains binary values, typically 0 or 1. They are often used to represent categorical features with only two possible values. For instance, in sentiment analysis, a binary vector can be used to indicate whether a sentiment is positive (1) or negative (0).
4. One-Hot Vectors: One-hot vectors are a special type of binary vector where only one element is 1, and the rest are 0. They are commonly used to represent categorical variables with multiple classes. Each element in the vector corresponds to a specific class, and the value 1 in the corresponding element indicates the presence of that class. For example, in a dataset of animal types, a one-hot vector can represent whether an animal is a dog, cat, or bird.
5. Sparse Vectors: In some datasets, the number of features can be very large, resulting in vectors with many zero elements. Sparse vectors are a memory-efficient representation that only stores the non-zero elements and their corresponding indices. This format is beneficial for reducing storage space and speeding up computations in situations where the majority of the features are zero.

These are just a few examples of the types of vectors used in machine learning. Each type serves a specific purpose in representing and processing data, allowing machine learning algorithms to effectively learn from and make predictions on various types of datasets.

Features of Vectors in Machine Learning

Vectors play a crucial role in machine learning, offering several features that make them well-suited for representing and processing data. Here are some notable features of vectors in machine learning:

1. Compact Representation: Vectors provide a compact and efficient way to represent complex data. By organizing information into a structured array of numeric values, vectors condense multiple attributes or features into a single object. This compact representation simplifies the storage and processing of data, enabling machine learning algorithms to handle large datasets efficiently.
2. Dimensionality: Vectors can have any number of dimensions, allowing them to represent data in multidimensional spaces. This feature is particularly valuable when dealing with datasets containing numerous attributes or features. Higher-dimensional vectors enable machine learning algorithms to capture and analyze relationships and patterns among multiple variables simultaneously.
3. Mathematical Operations: Vectors support various mathematical operations, such as addition, subtraction, and scalar multiplication. These operations allow for the manipulation and transformation of data stored in vectors, facilitating tasks such as data normalization, feature scaling, and similarity calculations. Mathematical operations on vectors form the basis of many machine learning algorithms.
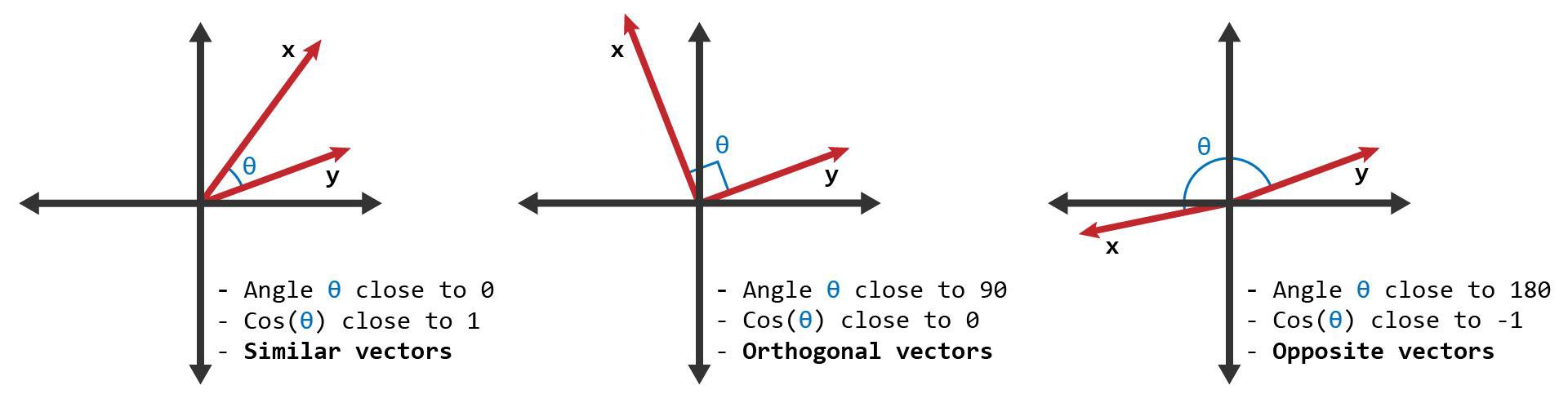
4. Distance Metrics: Vectors can be used to measure the similarity or dissimilarity between data points using distance metrics. Common distance metrics, such as Euclidean distance or cosine similarity, rely on the coordinates of vectors to quantify the proximity between them. Distance metrics enable machine learning algorithms to compare and group similar data points, aiding in clustering and classification tasks.
5. Flexible Representations: Vectors offer flexibility in representing different types of data. Whether the data is continuous or discrete, numerical or categorical, vectors can be adapted to accommodate various data types. This flexibility allows machine learning algorithms to handle diverse datasets, ranging from images and text to sensor readings and financial data.
6. Efficient Computation: Vectors enable efficient computation due to their alignment with hardware optimizations. Modern processors are equipped with vectorized instructions that can perform operations on multiple elements of a vector simultaneously, known as SIMD (Single Instruction, Multiple Data) operations. Leveraging these hardware capabilities allows for accelerated processing of large datasets, leading to faster training and inference in machine learning models.

These features make vectors a versatile and powerful tool in machine learning, enabling the representation, manipulation, and analysis of data in a way that facilitates the development and application of effective machine learning algorithms.

Vector Operations in Machine Learning

Vectors in machine learning support a variety of operations that are essential for data manipulation and algorithm development. These operations enable the processing and transformation of vectors, facilitating various tasks in machine learning. Here are some common vector operations used in machine learning:

1. Addition: Addition is a fundamental operation on vectors where corresponding elements of two vectors are summed together. This operation is often used in tasks such as feature combination and weighting, where multiple vectors need to be combined or averaged to create a new vector.
2. Subtraction: Subtraction allows for the computation of the difference between corresponding elements of two vectors. It is commonly used in tasks such as calculating the residuals or errors in regression models and evaluating the performance of machine learning algorithms.
3. Scalar Multiplication: Scalar multiplication involves multiplying a vector by a scalar, which scales each element of the vector by the scalar value. This operation is used in tasks such as feature scaling and normalization, where vectors are adjusted to have consistent ranges or magnitudes.
4. Dot Product: The dot product, also known as the inner product or scalar product, calculates the sum of the products of corresponding elements of two vectors. This operation is used to quantify the similarity between two vectors and is a key component in various machine learning algorithms, including linear regression and support vector machines.
5. Cross Product: The cross product is a vector operation specific to three-dimensional vectors. It produces a new vector that is perpendicular to the two input vectors. The cross product is commonly used in tasks involving geometry, such as calculating normal vectors or determining orientation.
6. Normalization: Normalization is a process in which vectors are rescaled to ensure that their magnitudes or lengths are equal. This operation is useful in tasks that require comparing vectors based on their direction rather than their magnitude, such as in cosine similarity calculations.
7. Distance Metrics: Distance metrics, such as Euclidean distance and cosine similarity, quantify the similarity or dissimilarity between two vectors. These metrics enable tasks such as clustering, nearest neighbor search, and evaluating the performance of machine learning models.

These vector operations provide the foundation for many machine learning algorithms and tasks. By leveraging these operations, researchers and practitioners can manipulate, compare, and transform vectors to extract meaningful insights and develop accurate predictive models.

Applications of Vectors in Machine Learning

Vectors are utilized in various machine learning applications to represent and process data efficiently. Their ability to capture and organize complex information in a structured format enables machine learning algorithms to extract patterns and make accurate predictions. Here are some key applications of vectors in machine learning:

1. Image Classification: In computer vision tasks, vectors are commonly used to represent images. Each pixel in an image can be considered a feature, and the values of these pixels form a vector that represents the image. Machine learning algorithms can learn from these vectors to classify images into different categories, such as identifying objects or recognizing facial expressions.
2. Natural Language Processing: Vectors play a crucial role in natural language processing (NLP) tasks, such as sentiment analysis and text classification. Techniques like word embeddings, such as Word2Vec or GloVe, map words to high-dimensional vectors, capturing semantic relationships between words. These vectors enable algorithms to understand and analyze textual data, making NLP applications more efficient and accurate.
3. Recommendation Systems: Vectors are vital in recommendation systems that suggest products, movies, or content based on user preferences. User vectors are created by representing their past interactions or preferences, such as ratings or click history. By comparing these user vectors to item vectors, algorithms can provide personalized recommendations that match user interests and preferences.
4. Anomaly Detection: Vectors are used to detect anomalies or outliers in datasets. Anomaly detection algorithms compare the vector representations of data points to a learned distribution, identifying instances that deviate significantly from the norm. This is useful in various applications, such as fraud detection, network intrusion detection, or equipment failure prediction.
5. Clustering: Vectors are used in clustering algorithms to group similar data points together. By comparing the distances or similarities between vectors, clustering algorithms can identify cohesive groups or clusters within a dataset. This has applications in customer segmentation, market research, and image segmentation, among others.
6. Dimensionality Reduction: Vectors can be used in dimensionality reduction techniques such as Principal Component Analysis (PCA) and t-SNE. These techniques transform high-dimensional data into lower-dimensional vectors, capturing the most informative features while preserving relationships between data points. Dimensionality reduction is useful for visualization, reducing computational complexity, and improving model performance.
7. Regression Analysis: Vectors are used to represent the input features in regression models, where the goal is to predict a continuous output. Each element of the input vector corresponds to a specific feature, and the algorithm learns the relationships between these features and the target variable. Regression analysis is applied in various fields, such as sales forecasting, demand prediction, and financial modeling.

These are just a few examples of the broad range of applications where vectors are utilized in machine learning. Their versatility and effectiveness in representing and processing data make them indispensable in numerous domains, driving advancements in artificial intelligence and data analytics.

Conclusion

Vectors play a fundamental role in machine learning, providing a compact and efficient way to represent and process data. They serve as a versatile tool for organizing and manipulating complex information, enabling machine learning algorithms to extract patterns, make accurate predictions, and gain insights from diverse datasets.

Throughout this article, we have explored the definition of vectors in the context of machine learning, discussed various types of vectors, and highlighted their features and operations. Vectors are essential for representing both input features and output targets in machine learning tasks. They allow for efficient computation, support mathematical and distance-based operations, and provide flexible representations for different types of data.

Moreover, vectors find applications in a wide range of machine learning tasks and domains. They are used in image classification, natural language processing, recommendation systems, anomaly detection, clustering, dimensionality reduction, regression analysis, and many other applications. By leveraging the power of vectors, machine learning algorithms can make accurate predictions, provide personalized recommendations, detect anomalies, and gain valuable insights from vast amounts of data.

In summary, vectors are a crucial component of machine learning, facilitating the representation, manipulation, and analysis of data. Their ability to compactly capture information, support mathematical operations, and enable efficient computation underpins the advancements in machine learning and artificial intelligence. Embracing the potential of vectors will undoubtedly continue to drive innovation and improve the performance of machine learning algorithms in various domains and applications.