What Is Graph Machine Learning

Introduction

Graph Machine Learning (GML) is a rapidly evolving field that combines elements of graph theory and machine learning to make sense of complex data. In recent years, there has been a significant increase in the amount of interconnected and structured data available, ranging from social networks to biological systems. Traditional machine learning techniques struggle to effectively analyze and extract meaningful insights from this type of data due to its interconnected nature.

GML, on the other hand, leverages the power of graph theory to model and analyze relationships between entities in a dataset. By representing data as graphs, with nodes representing entities and edges representing connections or relationships between them, GML enables the extraction of valuable information, patterns, and predictions.

One of the defining characteristics of GML is its ability to capture both local and global relationships within a dataset. This is particularly valuable in scenarios where understanding the interconnectedness of data points is essential. For example, GML can be used to analyze social networks, where relationships between individuals play a crucial role in understanding their behavior and social dynamics.

GML has gained significant attention in recent years due to its wide range of applications across various domains. Whether it’s analyzing citation networks in academia, predicting drug-target interactions in drug discovery, or identifying communities in social networks, GML provides powerful tools to unearth valuable insights from complex data.

However, GML is not without its challenges. The sheer size and complexity of graph datasets can pose computational challenges, requiring the development of efficient algorithms and scalable methods. Additionally, the lack of labeled data for training purposes and the need for interpretability and explainability in GML models present further obstacles.

In this article, we will delve into the world of GML, exploring its key concepts, common algorithms, and real-world applications. We will also discuss the challenges and limitations that researchers and practitioners face in the field. By the end, you will have a solid understanding of what GML is and why it is a valuable tool in the era of big data and interconnected systems.

What is Graph Machine Learning?

Graph Machine Learning (GML), also known as Graph Deep Learning or Graph Neural Networks, is a subfield of machine learning that focuses on analyzing and making predictions from data represented in the form of graphs. A graph is a mathematical structure composed of nodes (also known as vertices) and edges (also known as links or connections), which represent the relationships or interactions between the nodes. GML leverages these graph structures to capture and understand complex patterns and relationships in data.

Traditional machine learning algorithms are designed for analyzing tabular data, where each row represents an instance and each column represents a feature. However, many real-world datasets do not adhere to this tabular structure. Instead, they exhibit intricate interdependencies and connectivity among the data points, such as social networks, citation networks, biological networks, and knowledge graphs.

GML provides a framework to handle these interconnected datasets by augmenting traditional machine learning algorithms with graph-based techniques. It enables the integration of both structural information, encoded by the graph topology, and nodal features to generate powerful models that can reason about relationships, propagate information, and make predictions.

To apply GML, the graph data is typically transformed into a format suitable for machine learning algorithms. This can involve techniques such as node feature extraction, graph normalization, and graph convolution operations. The goal is to effectively model and learn from the graph structure while incorporating information from the individual nodes and their attributes.

One of the key advantages of GML is its ability to capture not only local relationships between adjacent nodes but also global dependencies across the graph. This allows GML models to leverage information from distant nodes or capture community structures, facilitating better predictions and insights.

Furthermore, GML overcomes the limitations of traditional machine learning algorithms when it comes to handling irregular and variable-sized data. Since the graph structure is flexible and scalable, GML can accommodate graphs of various sizes and shapes, making it suitable for analyzing datasets that exhibit dynamic or evolving relationships.

Overall, GML provides a powerful framework for analyzing and understanding complex, interconnected data. By harnessing the rich representation power of graphs and combining it with machine learning techniques, GML offers a sophisticated approach to extract insights, make predictions, and tackle real-world problems across various domains.

Why is Graph Machine Learning Important?

Graph Machine Learning (GML) is increasingly recognized as a valuable tool for analyzing and making predictions from graph-structured data. It addresses the limitations of traditional machine learning algorithms when it comes to capturing and utilizing the rich interconnections and relationships present in complex datasets. Here are several reasons why GML is important:

Capturing Relationship Dynamics: Many real-world systems and phenomena exhibit intricate relationships and dependencies that evolve over time. GML allows us to model and analyze the dynamics of these relationships, enabling us to understand how they change and adapt. This is essential in fields such as social networks, where the dynamics of friendships, collaborations, and influence play a crucial role.
Handling Heterogeneous Data: Graphs can represent a wide range of heterogeneous data types, such as text, images, and numerical attributes. GML provides a unified framework for incorporating and leveraging these diverse data modalities within the graph structure, allowing for more comprehensive and accurate analysis.
Uncovering Hidden Patterns and Insights: GML techniques can reveal hidden patterns and valuable insights that may not be apparent in traditional tabular datasets. By considering both the local and global connectivity of nodes, GML algorithms can identify communities, detect anomalies, and uncover unknown relationships, leading to a deeper understanding of complex systems.
Enhancing Predictive Power: Graph structures encode rich contextual information. By incorporating this information into machine learning models, GML can significantly enhance predictive performance. For example, in recommendation systems, GML can leverage the network of user-item interactions to make personalized recommendations with higher accuracy.
Enabling Transfer Learning: GML supports the transfer of knowledge from one graph domain to another. Pretrained models or learned representations from one graph can be transferred to related graphs, reducing the need for extensive training data and improving model generalization.

GML holds immense potential for a wide range of applications. It has demonstrated success in various domains, including social network analysis, bioinformatics, cybersecurity, recommendation systems, and knowledge graph analysis. By leveraging the power of graph structures, GML enables us to tackle real-world problems that involve complex relationships, dynamic interactions, and diverse types of data. As the availability and complexity of graph-structured datasets grow, GML will continue to play a vital role in unlocking valuable insights and advancing our understanding in diverse fields.

Key Concepts in Graph Machine Learning

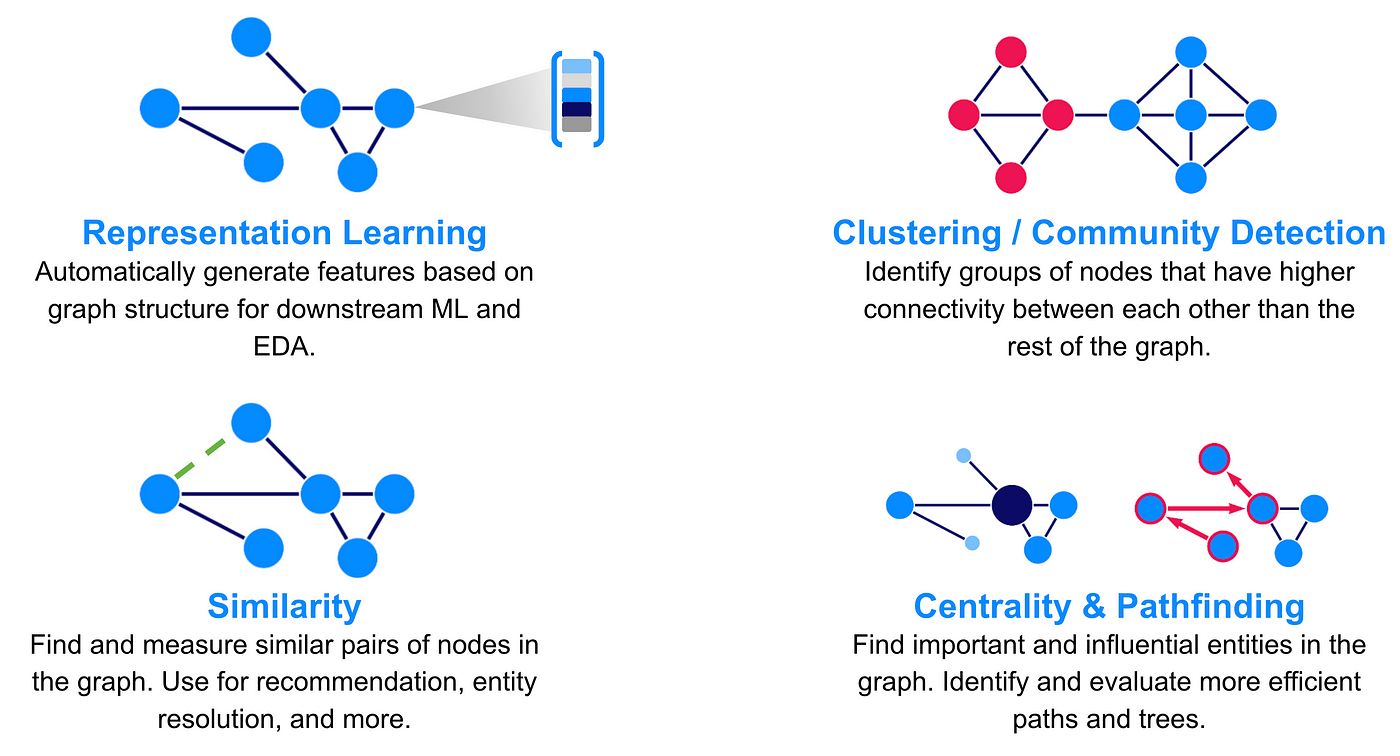
Graph Machine Learning (GML) encompasses several key concepts and techniques that are fundamental to understanding and applying this field. These concepts provide the foundation for modeling and analyzing graph-structured data. Here are some of the key concepts in GML:

Graph Representation: The graph is the fundamental structure in GML. It consists of nodes (also known as vertices) and edges (also known as links) that represent entities and their relationships, respectively. The nodes can have associated features or attributes that provide additional information about the entities.
Node Embeddings: Node embeddings encode the characteristics or properties of nodes into low-dimensional vectors. Embeddings capture both structural and attribute information, allowing nodes with similar characteristics to have similar embeddings. Node embeddings are crucial for feeding the data into machine learning models.
Graph Neural Networks (GNNs): GNNs are a class of machine learning models specifically designed for graph-structured data. GNNs operate on graphs by iteratively updating node embeddings based on the information from neighboring nodes. This enables GNNs to capture dependencies and relationships between nodes, thereby facilitating powerful graph-based predictions.
Graph Convolutional Networks (GCNs): GCNs are a popular type of GNN that apply convolutional operations on graphs. GCNs extend the concept of convolutions from regular grid-like structures (such as images) to graph structures, enabling the propagation of information through the graph and learning of local and global patterns.
Graph Pooling: Graph pooling is the process of aggregating nodes or subgraphs to reduce the size or resolution of the graph while preserving its essential features. Pooling allows efficient processing of large graphs and helps capture high-level representations and hierarchies in the data. Typical pooling techniques include graph coarsening and graph summarization.
Graph Attention Mechanism: Graph attention mechanisms enable GNNs to assign varying importance to different neighbors of a node. By assigning attention weights, GNNs can selectively focus on relevant neighbors and effectively leverage their information, improving the model’s performance in capturing meaningful relationships.
Graph Generation: Graph generation refers to the task of generating new graphs that possess similar properties to an input set of graphs. This task is essential in various applications, such as generating chemical compounds, simulating social networks, or generating realistic game environments.

These key concepts form the building blocks of GML and provide the necessary tools for modeling, analyzing, and generating graph-structured data. By understanding and utilizing these concepts, researchers and practitioners can develop powerful GML models that capture the rich relationships and dependencies in complex datasets.

Common Algorithms in Graph Machine Learning

Graph Machine Learning (GML) encompasses a range of algorithms that leverage the graph structure to analyze and make predictions from graph-structured data. These algorithms are specifically designed to capture the rich relationships and dependencies present in graphs. Here are some of the common algorithms used in GML:

Graph Convolutional Networks (GCNs): GCNs are one of the foundational algorithms in GML. They extend convolutional operations to graphs and learn node representations by aggregating information from neighboring nodes. GCNs leverage the graph structure to capture local and global patterns, making them effective for tasks such as node classification, link prediction, and graph classification.
Graph Attention Networks (GATs): GATs utilize attention mechanisms to selectively attend to different neighbors of a node, giving varying importance to their contributions. By attending to relevant neighbors, GATs can effectively capture dependencies and make more accurate predictions. GATs have been successful in applications such as recommendation systems, where attention weights help identify important user-item interactions.
Graph Autoencoders: Graph autoencoders encode graph data into low-dimensional latent vectors and then reconstruct the original graph structure. By learning compact representations, graph autoencoders can capture the essential features of a graph and enable tasks such as graph generation, anomaly detection, and graph clustering.
Graph Neural Networks (GNNs): GNNs represent a family of algorithms that operate on graphs. GNNs update node representations iteratively by aggregating and propagating information from neighboring nodes. This allows GNNs to capture complex relationships, learn from structural patterns, and make predictions on graph-structured data. GNNs have shown effectiveness in tasks such as link prediction, node classification, and community detection.
Graph Isomorphism Networks (GINs): GINs are a type of GNN that parameterizes the update function of a node’s representation based on the aggregation of neighbor node representations. GINs are powerful and expressive, capable of handling graphs with different sizes or structures. They have been successfully applied to various graph-related tasks, including molecule property prediction, social network analysis, and recommendation systems.
Graph Recurrent Networks (GRNs): GRNs extend the concept of recurrent neural networks to graph-structured data. GRNs capture temporal dependencies and dynamics in graphs by recurrently updating node representations based on the previous states and the graph structure. GRNs are particularly useful in modeling sequences of graphs, such as in dynamic social networks or time-evolving molecular structures.

These algorithms represent a subset of the wide range of techniques available in GML. Each algorithm has its strengths and limitations, and the choice of algorithm depends on the specific task and characteristics of the graph data. By leveraging these algorithms, researchers and practitioners can effectively analyze and extract meaningful insights from graph-structured data, paving the way for advancements in various fields.

Real-World Applications of Graph Machine Learning

Graph Machine Learning (GML) has found numerous applications across various domains, harnessing the power of graph structures to analyze and make predictions from complex interconnected data. Here are some real-world applications of GML:

Social Network Analysis: GML is extensively used in analyzing social networks, where individuals are represented as nodes and connections between them depict their relationships. GML algorithms can identify influential users, detect communities, predict links, and analyze information diffusion, enabling businesses to better understand user behavior, optimize marketing strategies, and detect anomalies.
Bioinformatics: GML has strong applications in bioinformatics, where graphs can represent biological networks such as protein-protein interactions, gene regulatory networks, or metabolic pathways. By analyzing these networks, GML can aid in predicting protein functions, identifying disease-related genes, designing new drugs, and understanding the underlying mechanisms of biological systems.
Recommendation Systems: GML algorithms can improve the accuracy and quality of recommendation systems by leveraging the graph structure of user-item interactions. By considering the connections between users and items, GML can make personalized recommendations, enhance customer satisfaction, and increase business revenue in domains such as e-commerce, music streaming, and social media.
Knowledge Graph Analysis: Knowledge graphs capture semantic relationships between entities, allowing for sophisticated knowledge representation and reasoning. GML techniques can analyze and enrich knowledge graphs, enabling tasks such as entity resolution, relation extraction, question answering, and ontology exploration. This facilitates advancements in areas such as natural language processing, information retrieval, and intelligent systems.
Cybersecurity: GML plays a vital role in cybersecurity by detecting and analyzing malicious activities in network data. GML algorithms can identify network intrusions, detect anomalies, uncover attack patterns, and predict potential threats. By using GML, cybersecurity professionals can enhance threat detection and response, safeguard critical infrastructure, and protect sensitive data.
Urban Planning and Transportation: GML can analyze transportation networks, city infrastructures, and spatial relationships to optimize urban planning, traffic management, and public transportation systems. Graph-based analysis allows for improved route planning, congestion prediction, urban development modeling, and smart city initiatives, leading to efficient and sustainable urban environments.

These are just a few examples of how GML is being applied in practical scenarios. The versatility of GML enables its use in various domains, including finance, healthcare, logistics, and social sciences. With the ever-increasing connectivity and complexity of data, GML continues to unlock valuable insights and drive advancements in real-world applications, ultimately improving decision-making, efficiency, and user experiences.

Challenges and Limitations of Graph Machine Learning

While Graph Machine Learning (GML) offers powerful tools for analyzing graph-structured data, it also faces several challenges and limitations that researchers and practitioners must address. Here are some of the key challenges in GML:

Scalability: The size and complexity of graph datasets pose significant computational challenges. Traditional machine learning techniques struggle to handle large-scale graphs efficiently. Developing scalable algorithms and techniques that can handle massive graph datasets remains a major research focus in GML.
Data Availability: Labeled graph data for training purposes is often limited compared to labeled tabular data. Collecting and curating labeled graphs can be expensive and time-consuming. The lack of sufficient labeled graph data hinders the development and training of accurate and robust GML models.
Interpretability: GML models often lack interpretability. Understanding how and why a GML model arrived at a certain prediction or decision is challenging, as the complex graph structures and hidden dependencies make it difficult to trace the reasoning process. Developing techniques to enhance the interpretability of GML models is an ongoing research area.
Generalization: Generalizing GML models to unseen graphs or domains can be challenging. GML models trained on one graph may not perform well on graphs with different characteristics or structures. Transfer learning techniques, domain adaptation, and graph augmentation methods are being explored to address this challenge and improve model generalization.
Noise and Incompleteness: Graph data often contains noise, missing information, or incomplete connections. Handling noisy or incomplete graphs is a challenge in GML, as errors or inaccuracies can propagate through the graph during information propagation or aggregation. Developing robust algorithms to handle noise and incompleteness in graph data is essential for accurate predictions and analysis.
Ethical Considerations: As with any machine learning field, GML raises ethical considerations. Understanding the ethical implications of using graph data, ensuring privacy and security of sensitive information, and addressing potential biases in GML models are crucial areas of concern that need to be addressed.

These challenges and limitations highlight the need for further research and development in GML. New algorithms, techniques, and frameworks are being devised to overcome these challenges and improve the effectiveness, scalability, interpretability, and ethical aspects of GML models. By addressing these limitations, GML can continue to evolve as a valuable tool for analyzing and extracting insights from complex graph-structured data.

Conclusion

Graph Machine Learning (GML) has emerged as a powerful field that combines graph theory and machine learning to analyze and make predictions from complex, interconnected datasets. By leveraging the inherent structure and relationships of graphs, GML offers rich insights into diverse domains, ranging from social networks and bioinformatics to recommendation systems and urban planning.

In this article, we explored the key concepts in GML, including graph representation, node embeddings, and graph neural networks. We discussed common algorithms used in GML, such as graph convolutional networks (GCNs), graph attention networks (GATs), and graph autoencoders. Additionally, we highlighted the real-world applications of GML in areas such as social network analysis, bioinformatics, and recommendation systems.

However, GML is not without its challenges and limitations. Scalability, limited labeled data, interpretability, generalization, and noise in graph data are areas that require further research and development. Additionally, ethical considerations related to privacy, security, and bias need to beaddressed in the context of GML.

Despite these challenges, GML holds immense promise in unlocking valuable insights and facilitating advanced data analysis in a wide range of fields. Continued research and advancements in GML algorithms, models, and interpretability techniques will pave the way for more accurate predictions, better understanding of complex systems, and improved decision-making.

As we move further into an era of big data and interconnected systems, GML will continue to play a critical role in extracting meaningful information from graph-structured data. By harnessing the power of graph structures and combining it with machine learning techniques, GML empowers us to gain deeper insights and make more informed decisions across various domains.