Introduction
Welcome to the world of machine learning, where artificial intelligence algorithms are designed to learn and make intelligent decisions. One such algorithm is the Perceptron. In this article, we will explore what a Perceptron is, how it works, and its applications in the field of machine learning.
The concept of a Perceptron was first introduced by Frank Rosenblatt in 1958. Inspired by the functioning of neurons in the human brain, the Perceptron is a basic building block of artificial neural networks. It serves as a binary classifier, making decisions by computing weighted sums of input features and applying a threshold function.
The Perceptron is extensively used in various fields, including image and speech recognition, natural language processing, and pattern classification. Understanding its working principles is essential for anyone interested in diving deeper into the realm of machine learning.
In this article, we will discuss the inner workings of a Perceptron, the Perceptron learning rule, the role of the bias unit, the activation function, and the process of training a Perceptron. We will also highlight the limitations of Perceptrons and provide insights into other more advanced neural network architectures.
Whether you are a beginner in machine learning or an experienced practitioner, this article will equip you with a solid understanding of the Perceptron and its significance in building intelligent systems.
What is a Perceptron
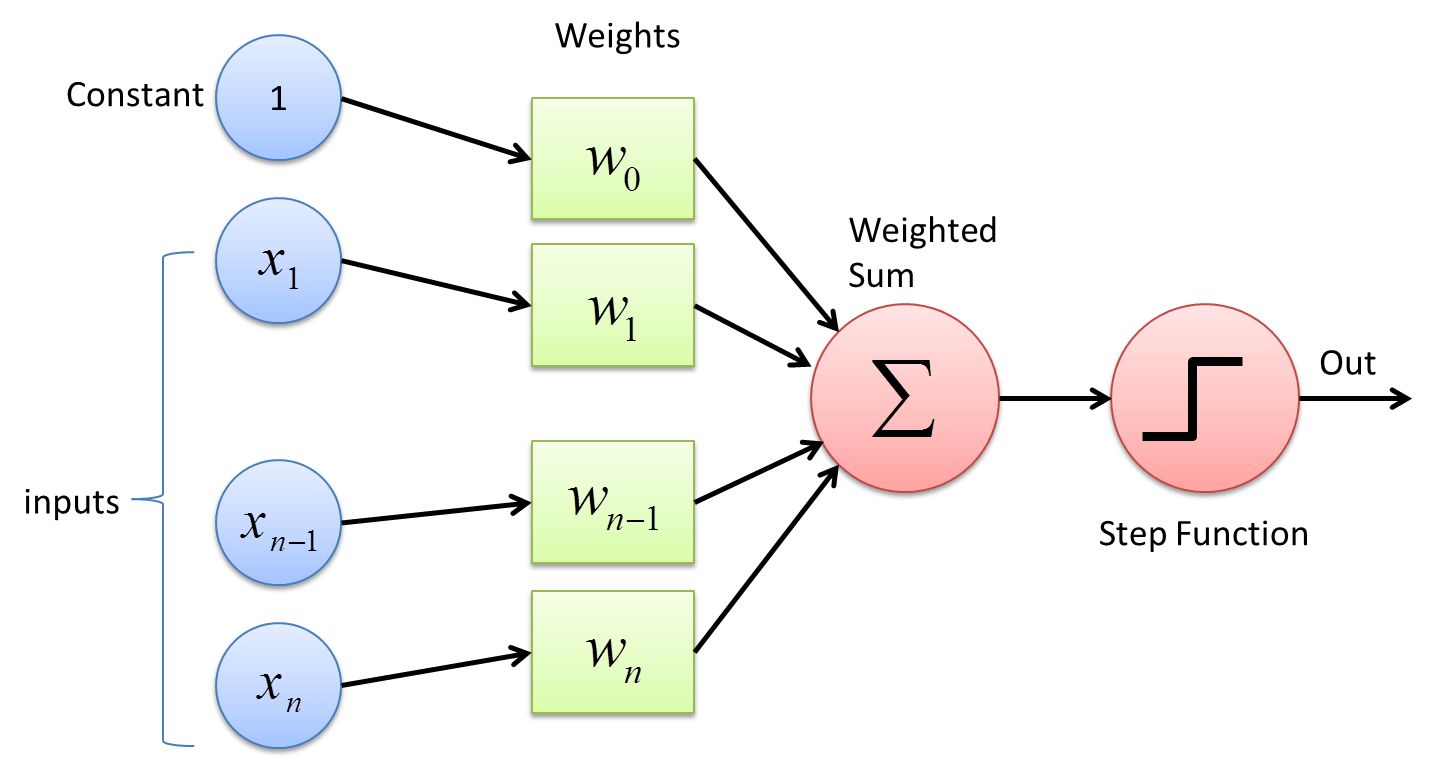
A Perceptron is a fundamental unit of computational models inspired by the functioning of neurons in the human brain. It is a type of artificial neural network that serves as a simple binary classifier, capable of making decisions based on input features.
At its core, a Perceptron takes a set of numerical inputs, assigns weights to them, computes a weighted sum, and applies an activation function to produce an output. The activation function helps determine whether the Perceptron should fire or remain inactive based on the weighted sum of inputs.
The Perceptron consists of three main components:
- Input Layer: This layer receives the input features, which can be real-valued numbers representing various attributes of the data.
- Weighted Sum: Each input feature is assigned a weight, which determines its importance in the decision-making process. The Perceptron computes the weighted sum of the inputs by multiplying each input with its corresponding weight.
- Activation Function: The weighted sum is passed through an activation function, which introduces non-linearity into the decision-making process. The activation function determines the firing or inactivity of the Perceptron based on the computed sum.
The Perceptron makes a binary decision by comparing the output of the activation function to a threshold value. If the output exceeds the threshold, the Perceptron fires and produces a positive output. Otherwise, it remains inactive and produces a negative output.
Each Perceptron is designed to learn from the input data by adjusting its weights during the training process. This enables the Perceptron to make predictions and classify new, unseen data based on patterns learned from the training data.
In the next section, we will delve deeper into the working principles of a Perceptron and understand how it makes decisions based on the weighted inputs and activation function.
How does a Perceptron Work
To understand how a Perceptron works, let’s take a closer look at its inner workings and decision-making process.
A Perceptron takes a set of input features, each of which is assigned a weight that represents its importance in the decision-making process. The Perceptron computes the weighted sum of the inputs by multiplying each input with its corresponding weight.
Mathematically, the weighted sum (z) can be represented as:
z = w₁x₁ + w₂x₂ + … + wₙxₙ
where w₁, w₂, …, wₙ are the weights assigned to the input features x₁, x₂, …, xₙ.
Once the weighted sum is computed, it is passed through an activation function. The activation function introduces non-linearity into the decision-making process and determines the output of the Perceptron.
There are various types of activation functions that can be used in a Perceptron, including step function, sigmoid function, hyperbolic tangent (tanh) function, and rectified linear unit (ReLU) function.
For example, the step function is a popular activation function used in binary classification problems. It takes the weighted sum as input and outputs a 1 if the sum is greater than or equal to a threshold value, and it outputs a 0 otherwise.
The decision-making process of a Perceptron can be summarized as follows:
- Receive input features and assigned weights.
- Compute the weighted sum of the inputs.
- Pass the weighted sum through an activation function.
- If the output of the activation function exceeds a threshold value, the Perceptron fires and produces a positive output. Otherwise, it remains inactive and produces a negative output.
Through training, a Perceptron learns from a labeled dataset by adjusting its weights iteratively. This adjustment is based on the error between the predicted output and the correct output. By minimizing the error, the Perceptron fine-tunes its weights to make more accurate predictions.
In the next section, we will explore the Perceptron learning rule in more detail and understand how the weights are updated during the training process.
Perceptron Learning Rule
The Perceptron learning rule is a key component of training a Perceptron. It allows the Perceptron to adjust its weights iteratively and learn from labeled training data in order to make accurate predictions.
During the training process, the Perceptron takes an input feature vector and computes the weighted sum of the inputs. It then compares the output of the activation function to the expected output. If the predicted output matches the expected output, no adjustments are made to the weights.
However, if the predicted output is different from the expected output, the weights are updated according to the Perceptron learning rule. The rule states that the weights should be adjusted in the direction that brings the predicted output closer to the expected output.
The weight update formula for the Perceptron learning rule is as follows:
wᵢ(new) = wᵢ(old) + α(y – ŷ)xᵢ
where wᵢ(new) is the updated weight, wᵢ(old) is the previous weight, α (alpha) is the learning rate, y is the expected output, ŷ is the predicted output, and xᵢ is the input feature.
The learning rate (α) determines the step size in adjusting the weights. It is a hyperparameter that needs to be carefully chosen to strike a balance between convergence speed and stability. A high learning rate may result in fast convergence, but it can also make the Perceptron unstable. On the other hand, a low learning rate may lead to slow convergence or getting stuck in local minima.
The learning process continues iteratively until the Perceptron achieves a satisfactory level of accuracy or reaches a predetermined maximum number of iterations. The Perceptron learning rule allows the Perceptron to update its weights incrementally, allowing it to learn and adapt to the patterns present in the training data.
In the next section, we will discuss the role of the bias unit in a Perceptron and its importance in the decision-making process.
Bias Unit
In a Perceptron, the bias unit plays a crucial role in the decision-making process and allows the model to make more accurate predictions. It is an additional input feature that is not directly connected to any specific input, but it influences the output of the Perceptron.
The bias unit is represented by a fixed weight (w₀) and is always set to the value of 1. It acts as a constant factor that allows the Perceptron to adjust the decision boundary or threshold for activation. The bias unit helps the Perceptron make better predictions by accounting for any inherent bias or preference in the input data.
Mathematically, the weighted sum (z) with the bias unit can be represented as:
z = w₀ + w₁x₁ + w₂x₂ + … + wₙxₙ
where w₀ is the weight of the bias unit and x₁, x₂, …, xₙ are the input features.
By incorporating a bias unit, the decision boundary of the Perceptron is shifted, allowing for better separation between classes in the input data space. This flexibility helps the Perceptron be more expressive and make accurate predictions even when the input features do not naturally align with the ideal decision boundary.
During the training process, the weight of the bias unit is also subject to adjustment based on the Perceptron learning rule. It is updated along with the weights corresponding to the input features, ensuring that the bias unit contributes to the overall weight adjustments.
The bias unit allows the Perceptron to learn and adapt to the bias present in the data, enabling it to make more robust and accurate predictions. Without the bias unit, the Perceptron might struggle to capture certain patterns or biases in the data, resulting in suboptimal performance.
In the next section, we will discuss the activation function used in a Perceptron and its role in determining the output based on the weighted sum of inputs.
Activation Function
In a Perceptron, the activation function plays a vital role in determining the output based on the weighted sum of inputs. It introduces non-linearity into the decision-making process and helps the Perceptron make more complex and nuanced predictions.
There are several types of activation functions that can be used in a Perceptron, each with its own characteristics and suitability for different types of problems. Some commonly used activation functions include:
- Step function: The step function is a basic activation function that maps the weighted sum to a binary output. It outputs 1 if the weighted sum is greater than or equal to a threshold value, and 0 otherwise.
- Sigmoid function: The sigmoid function is a popular choice for activation in Perceptrons. It squashes the weighted sum to a range between 0 and 1, providing a smooth and continuous output. The sigmoid function is especially useful in problems where the output needs to be interpreted as a probability.
- Hyperbolic tangent (tanh) function: The hyperbolic tangent function is similar to the sigmoid function but maps the weighted sum to a range between -1 and 1. It is symmetric around the origin and allows for negative outputs, making it suitable for problems where the desired output can range from negative to positive values.
- Rectified Linear Unit (ReLU) function: The rectified linear unit function is widely used in neural networks, including Perceptrons. It outputs the weighted sum if it is positive, and 0 otherwise. This activation function introduces sparsity and can speed up the learning process of the Perceptron.
The choice of activation function depends on the nature of the problem and the desired behavior of the Perceptron. It is important to select an activation function that allows the Perceptron to effectively model the underlying patterns in the data and make accurate predictions.
By applying the activation function to the weighted sum, the Perceptron produces the final output. If the output exceeds a threshold value, the Perceptron fires and produces a positive output. Otherwise, it remains inactive and produces a negative output.
The activation function transforms the linear computation of the weighted sum into a non-linear decision boundary, enabling the Perceptron to learn and make complex predictions. It brings flexibility and expressive power to the Perceptron architecture, allowing it to capture intricate patterns present in the input data.
In the next section, we will discuss the process of training a Perceptron and how it adjusts its weights to improve its predictive capabilities.
Training a Perceptron
The process of training a Perceptron involves iteratively adjusting its weights to improve its ability to make accurate predictions. The goal is to minimize the error between the predicted output and the expected output for a given set of input data.
To train a Perceptron, you need a labeled dataset where each data point is associated with a known class or category. The training data consists of input features and their corresponding expected outputs. During training, the Perceptron takes the input features, computes the weighted sum, and applies the activation function to produce a predicted output.
If the predicted output matches the expected output, no weight adjustments are made. However, if the predicted output differs from the expected output, the weights are updated according to the Perceptron learning rule, as discussed earlier.
The weight update process is repeated for each data point in the training dataset until the Perceptron achieves a satisfactory level of accuracy or convergence. The convergence occurs when the Perceptron reaches a point where it consistently makes correct predictions for the given training data.
It’s important to note that the training of a Perceptron is an iterative process. The steps of calculating the weighted sum, applying the activation function, comparing the predicted output with the expected output, and updating the weights are repeated multiple times until the Perceptron learns the underlying patterns in the data.
The number of iterations required for training can vary depending on factors such as the complexity of the problem, the size of the training dataset, and the learning rate. It may take some trial and error to find the optimal number of iterations for a given problem.
Once the Perceptron is trained, it can be used to make predictions on new, unseen data. The learned weights are utilized to compute the weighted sum and apply the activation function to classify the input as belonging to a specific category or class.
Training a Perceptron is the initial step in building a powerful neural network. It sets the foundation for more complex models and algorithms that utilize multiple layers of interconnected Perceptrons, known as multi-layer perceptrons or artificial neural networks.
In the next section, we will discuss the limitations of Perceptrons and explore other advanced neural network architectures.
Limitations of Perceptrons
While Perceptrons are powerful and versatile machine learning algorithms, they come with certain limitations that must be considered when applying them to real-world problems. Understanding these limitations helps determine when it is appropriate to use Perceptrons or when more complex neural network architectures are needed.
One significant limitation of Perceptrons is their inability to solve problems that are not linearly separable. A linearly separable problem is one in which the classes or categories can be separated by a straight line or a hyperplane in higher dimensions. If a problem requires a non-linear decision boundary, Perceptrons alone cannot accurately model and classify the data.
Another limitation is that Perceptrons are only capable of binary classification. They can classify data into two categories, but they struggle with multi-class classification problems. However, this limitation can be overcome by using multiple Perceptrons in combination or by using more advanced neural network architectures such as multi-layer perceptrons.
The convergence of Perceptrons depends on the linear separability of the problem and the initial configuration of weights. In some cases, Perceptrons may fail to converge or may converge to a suboptimal solution. This issue can be addressed by using appropriate initialization techniques, adjusting the learning rate, or exploring more advanced optimization algorithms.
Perceptrons are also sensitive to outliers in the data. A single outlier can significantly impact the decision boundary and skew the predictions. Preprocessing the data to handle outliers or using robust training algorithms can mitigate this sensitivity.
Additionally, Perceptrons are not able to learn complex patterns or extract high-level features from the input data. They rely solely on the weighted sum of the input features, which limits their ability to capture intricate relationships in the data. This problem can be resolved by using more sophisticated neural network architectures that incorporate hidden layers and activation functions like convolutional neural networks or recurrent neural networks.
Despite these limitations, Perceptrons remain an important building block in the field of machine learning. They provide a foundation for understanding and implementing more advanced neural network architectures and serve as a starting point for learning about the principles and algorithms of artificial neural networks.
In the next section, we will summarize the key points discussed and provide final thoughts on Perceptrons and their role in machine learning.
Conclusion
In conclusion, Perceptrons are fundamental units of computational models inspired by the functioning of neurons in the human brain. They serve as simple binary classifiers and play a crucial role in the field of machine learning.
Throughout this article, we have explored various aspects of Perceptrons, starting from what they are to how they work. We have learned that Perceptrons compute a weighted sum of input features, pass it through an activation function, and make decisions based on the output. We have also discussed the Perceptron learning rule and how it allows the model to adjust its weights iteratively during the training process.
Moreover, we have highlighted the significance of the bias unit and the activation function in the decision-making process of Perceptrons. The bias unit helps capture bias in the data, while the activation function introduces non-linearity to enable more complex predictions.
While Perceptrons have their limitations, such as their inability to handle non-linearly separable problems and the challenge of multi-class classification, they serve as the foundation for more advanced neural network architectures. These advanced architectures, such as multi-layer perceptrons, convolutional neural networks, and recurrent neural networks, address the limitations of Perceptrons and enable us to solve more complex and real-world problems.
As you delve deeper into the field of machine learning, understanding Perceptrons and their principles will provide you with a solid foundation. They allow you to grasp the core concepts of neural networks and pave the way for exploring more advanced algorithms and models.
In summary, Perceptrons are important components in machine learning, serving as building blocks for more complex neural networks. They provide us with insights into the functioning of neurons and allow us to develop models that can learn and make intelligent decisions. So, keep exploring, experimenting, and utilizing the power of Perceptrons in your machine learning endeavors.