Introduction
Welcome to the world of machine learning, where algorithms and data drive insights and predictions! Machine learning, a subset of artificial intelligence, is revolutionizing various industries and powering innovations. At the core of machine learning lies the concept of feature vectors, which play a crucial role in extracting relevant information and enabling accurate predictions from data.
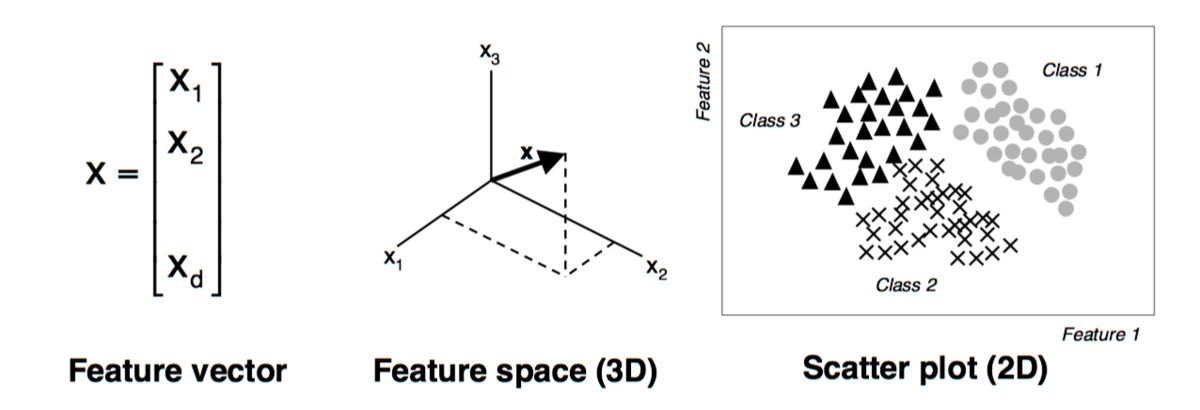
A feature vector is a numerical representation of an object or data point in machine learning. It is a mathematical representation of the features or attributes that describe the object or data point. These features can be anything from numerical values, categorical data, text, images, or even audio. By extracting and transforming these features into a structured format, machine learning algorithms can effectively discern patterns, identify similarities or differences, and make predictions or classifications.
The importance of feature vectors in machine learning cannot be overstated. They serve as the foundation upon which models are built and predictions are made. By capturing the essential characteristics of the data, feature vectors enable algorithms to generalize and make accurate predictions on unseen data.
Creating effective feature vectors involves careful consideration of the problem domain, domain knowledge, and the specific requirements of the machine learning task. It requires a combination of feature selection, feature engineering, and preprocessing techniques to extract relevant information and represent it in a way that best captures the underlying patterns.
In this article, we will explore the process of creating feature vectors, the common features used in machine learning, and various feature engineering techniques. We will also discuss the importance of scaling and normalization in feature vectors and explore different feature selection methods. So, let’s dive into the fascinating world of feature vectors in machine learning and discover how they enable the construction of powerful predictive models.
What is a Feature Vector?
In the context of machine learning, a feature vector is a numerical representation that captures the essential characteristics of an object or data point. It consists of a set of features or attributes that describe the object. These features can be quantitative, categorical, or even textual.
To understand the concept of a feature vector better, let’s consider an example. Suppose we want to build a spam email classifier. We can start by defining a set of features that help classify an email as spam or non-spam. These features may include the presence of certain keywords, the number of exclamation marks in the subject line, the sender’s domain, and the length of the email text. Each of these features forms a component of the feature vector.
The feature vector serves as a bridge between the raw data and the machine learning algorithm. It transforms the unstructured data into a structured format that the algorithm can understand and utilize for training and making predictions. By organizing the features into a vector, we create a concise representation that captures the necessary information while eliminating noise and irrelevant details.
In practice, a feature vector is typically represented as a one-dimensional array or vector. Each element of the vector corresponds to a specific feature and contains its corresponding value or encoding. For example, in our spam email classifier, the feature vector might look like [0, 3, 1, 342]. Here, the first element represents the presence of a particular keyword (0 for absent, 1 for present), the second element represents the number of exclamation marks, the third element represents the sender’s domain (encoded as a categorical value), and the fourth element represents the length of the email text.
The size of the feature vector depends on the number of features we choose to include. The more features we consider, the larger the feature vector becomes. It is important to note that not all features are equally informative, and the selection of relevant features is a crucial step in creating effective feature vectors.
Feature vectors are fundamental to machine learning as they enable algorithms to learn patterns, make predictions, and perform various tasks such as classification, regression, anomaly detection, and clustering. By extracting and representing the relevant features accurately, feature vectors provide the necessary input for machine learning models to generalize and make accurate predictions on new, unseen data.
Importance of Feature Vectors in Machine Learning
Feature vectors play a crucial role in machine learning as they are the building blocks of models and the key to making accurate predictions. Let’s explore the importance of feature vectors in more detail.
1. Information Extraction: The primary purpose of feature vectors is to extract relevant information from the data. By representing the features of an object or data point in a numerical format, machine learning algorithms can effectively process and analyze the data. Feature vectors encode the necessary details and patterns, enabling algorithms to learn and make informed decisions.
2. Dimensionality Reduction: In real-world applications, datasets can be vast and complex, with numerous features. Feature vectors help in reducing the dimensionality of the data by selecting the most relevant features. This process not only reduces computational complexity but also minimizes the risk of overfitting and improves the model’s generalization abilities.
3. Generalization and Prediction: Machine learning models aim to generalize patterns from the training data and make predictions on unseen data. Feature vectors provide the input necessary for models to learn and make accurate predictions. By representing the essential characteristics of the data, feature vectors enable models to discover underlying patterns and relationships, facilitating accurate predictions.
4. Feature Engineering: Feature vectors are the outcome of feature engineering, which involves selecting, transforming, and creating features based on domain knowledge. By carefully engineering feature vectors, practitioners can enhance the model’s performance by including insightful and discriminative features. This process requires a deep understanding of the problem domain and the ability to extract meaningful information from the data.
5. Interpretability: Feature vectors also aid in interpreting the model’s decisions. By analyzing the weights or importance assigned to each feature in the vector, we can gain insights into which aspects of the data contribute most to the model’s predictions. This interpretability is crucial in many real-world applications where transparency and explainability are essential.
6. Transferability: Feature vectors can be used across multiple machine learning models or tasks. Once feature engineering is performed and the feature vector is constructed, it can be reused with different algorithms or applied to related problems. This transferability saves time and effort by avoiding repetitive feature engineering for each new task.
In summary, feature vectors are the backbone of machine learning. They enable the extraction and representation of relevant information, reduce dimensionality, facilitate generalization and prediction, aid in feature engineering, provide interpretability, and offer transferability across models and tasks. The careful construction of feature vectors is crucial to ensure the effectiveness of machine learning models and their ability to deliver accurate and insightful predictions.
Creating Feature Vectors
Creating effective feature vectors is a critical step in machine learning. It involves transforming raw data into a structured numerical representation that captures the essential characteristics of the objects or data points. Let’s explore the process of creating feature vectors in more detail.
1. Identify Relevant Features: The first step is to understand the problem domain and identify the features that are most relevant to the task at hand. This requires domain knowledge and a deep understanding of the data. Depending on the nature of the problem, the features can be numerical, categorical, text-based, or even derived from other features.
2. Data Preprocessing: Once the relevant features are identified, the next step is to preprocess the data. This involves handling missing values, handling outliers, normalizing numerical features, and encoding categorical features. Data preprocessing ensures that the data is in a suitable format for further processing and feature extraction.
3. Feature Engineering: Feature engineering refers to the process of creating new features or transforming existing ones to enhance the predictive power of the model. This can involve techniques such as scaling, dimensionality reduction, polynomial expansion, encoding textual data, or creating interaction terms. Feature engineering requires domain knowledge and creativity to extract meaningful information from the data.
4. Construct the Feature Vector: With the relevant features identified and the data preprocessed and engineered, it’s time to construct the feature vector. This involves combining the features into a single vector representation. The size of the feature vector depends on the number of features selected. Each element in the vector corresponds to a specific feature, with its value or encoding.
5. Scaling and Normalization: It is often necessary to scale or normalize the feature vector to ensure that all features have a similar range or distribution. This is particularly important for machine learning algorithms that are sensitive to variations in feature magnitudes. Scaling and normalization help prevent certain features from dominating the learning process and ensure a fair contribution from all features.
6. Feature Selection: In some cases, not all features are equally informative or contribute significantly to the predictive performance of the model. Feature selection techniques can be employed to identify the most relevant features and discard redundant or irrelevant ones. This helps simplify the model, improve computational efficiency, and reduce the risk of overfitting.
7. Iterative Process: Creating feature vectors is an iterative process. It involves experimenting with different feature combinations, engineering techniques, and selection methods to find the optimal set of features. This process may require multiple iterations and continuous evaluation of the model’s performance.
In summary, creating feature vectors involves identifying relevant features, preprocessing the data, applying feature engineering techniques, constructing the feature vector, scaling and normalizing the features, and potentially selecting the most informative features. By carefully constructing feature vectors, we can extract meaningful information from the data and provide the necessary input for machine learning models to make accurate predictions.
Common Features in Machine Learning
In machine learning, various types of features are commonly used to capture the characteristics of objects or data points. These features serve as inputs to the machine learning algorithms and play a vital role in the model’s ability to learn and make predictions. Let’s explore some of the common features used in machine learning.
1. Numerical Features: Numerical features are quantitative measurements that represent numerical values. They can be continuous or discrete. Examples of numerical features include age, temperature, height, or any other measurable quantity. Numerical features provide valuable information about the magnitude or quantity of an attribute.
2. Categorical Features: Categorical features represent qualitative attributes that fall into distinct categories or classes. These features do not have an inherent order or magnitude. Examples of categorical features include gender, color, country, or any other attribute that can be classified into different categories. Categorical features provide information about the class or category to which an object belongs.
3. Textual Features: Textual features involve the analysis and representation of textual data. This can include techniques such as bag-of-words representation, TF-IDF (term frequency-inverse document frequency), or word embeddings. Textual features capture the semantic meaning or context of text, allowing algorithms to analyze and understand language patterns.
4. Image Features: Image features represent the visual characteristics of an image. These features can include pixel values, color histograms, or deep learning-based features extracted from pre-trained convolutional neural networks. Image features capture the visual patterns and content within an image, enabling algorithms to perform tasks such as object detection, image classification, or image retrieval.
5. Temporal Features: Temporal features capture the time-dependent nature of data. These features can include date, time, or temporal patterns. Temporal features are crucial in time series analysis, forecasting, or any problem where the temporal dimension plays a significant role.
6. Geospatial Features: Geospatial features pertain to geographical or spatial information. These features can include latitude, longitude, distance, or spatial patterns. Geospatial features enable algorithms to analyze patterns or relationships in data that are geographically distributed or have a spatial component.
7. Derived Features: Derived features are created by applying mathematical or logical operations on existing features. For example, calculating the ratio between two numerical features or creating interaction terms can be considered derived features. Derived features help capture complex relationships between features and provide additional information that may enhance the model’s predictive power.
It’s important to note that the selection of features depends on the problem domain, data characteristics, and the specific goals of the machine learning task. The combination of different types of features can provide a holistic representation of the data and enable algorithms to learn patterns and make accurate predictions.
In summary, common features in machine learning include numerical, categorical, textual, image, temporal, geospatial, and derived features. By utilizing a combination of these features, machine learning models can capture the relevant characteristics of the data and make informed predictions.
Feature Engineering Techniques
Feature engineering is a vital process in machine learning that involves manipulating and transforming raw data to create more informative and representative features. By applying various feature engineering techniques, we can enhance the performance and predictive power of our machine learning models. Let’s explore some common feature engineering techniques:
1. Polynomial Features: Polynomial features involve creating new features by taking the interaction or combination of existing features up to a certain degree. This technique enables models to capture nonlinear relationships between features and can be particularly useful when the data exhibits complex patterns.
2. Feature Scaling: Feature scaling involves transforming numerical features to ensure they are on a similar scale. Common scaling techniques include standardization (mean = 0, standard deviation = 1) and normalization (scaling values to a specific range, such as [0, 1]). Scaling features can prevent certain features from dominating the learning process and improve the stability and convergence of models that rely on distance-based calculations.
3. One-Hot Encoding: One-hot encoding is widely used to handle categorical features. It involves representing categorical variables as binary vectors, with each possible category as a separate binary feature. This technique allows algorithms to process and utilize categorical information effectively, without assuming any ordinal relationships between categories.
4. Handling Missing Data: When dealing with missing data, it is essential to apply appropriate techniques to handle this issue. Common strategies include imputation, where missing values are estimated or replaced, or treating missing values as a separate category. The chosen approach depends on the nature of the data and the specific requirements of the problem.
5. Binning: Binning involves dividing continuous numerical features into discrete bins or intervals. This technique allows us to convert continuous data into categorical or ordinal representations, enabling algorithms to capture trends or patterns within specific ranges of the numerical values.
6. Feature Extraction from Text: Text data requires special techniques for feature engineering. This can involve applying techniques such as tokenization, stemming, or TF-IDF (term frequency-inverse document frequency) vectorization to convert text into numerical representations. Additionally, advanced techniques like word embeddings (such as Word2Vec or GloVe) can capture semantic relationships and similarities between words.
7. Feature Selection: Feature selection techniques aim to identify the most relevant and informative features for a given problem. This can involve analyzing the correlation between features, using statistical tests, or utilizing algorithms such as LASSO (least absolute shrinkage and selection operator) or recursive feature elimination. By selecting the most informative features, we can reduce the dimensionality of the problem and improve model performance.
These are just a few examples of the many feature engineering techniques available. The selection and application of these techniques depend on the specific dataset, problem domain, and the requirements of the machine learning task. By leveraging appropriate feature engineering techniques, we can transform raw data into meaningful and informative features, enabling machine learning models to gain deeper insights and make accurate predictions.
Scaling and Normalization of Feature Vectors
Scaling and normalization are important steps in feature engineering that ensure the features in a feature vector are on a similar scale and range. By scaling and normalizing feature vectors, we can improve the performance and stability of machine learning models. Let’s explore the significance of scaling and normalization in more detail.
1. Equalizing Feature Magnitudes: Features often have different magnitudes, units, or ranges. Machine learning algorithms that rely on distance-based calculations, such as k-nearest neighbors or support vector machines, can be biased towards features with larger magnitudes. Scaling and normalization techniques bring all features to a similar scale, ensuring that no single feature dominates the learning process.
2. Enhancing Convergence Speed: Scaling and normalization can improve the convergence speed of iterative optimization algorithms, such as gradient descent. When features have similar scales, the optimization process can converge more quickly, allowing the model to reach an optimal solution faster. This is especially beneficial in large-scale machine learning problems where computational efficiency is crucial.
3. Regularization and Weight Interpretability: Scaling and normalization can facilitate the interpretation of model weights. Regularization techniques, such as L1 or L2 regularization, penalize large weights. When features have different scales, regularization may affect the features with larger magnitudes more significantly, leading to biased modeling. Scaling and normalization help ensure that regularization is applied uniformly across all features, promoting fair weight regularization and improving the interpretability of the model.
4. Handling Outliers: Outliers can significantly affect the range and distribution of features. Scaling and normalization techniques can reduce the impact of outliers by transforming the data to a more standardized distribution. This helps prevent outliers from disproportionately influencing the learning process and improves the model’s robustness to extreme values.
5. Normalizing Distributions: Normalization techniques transform the feature vector to have a specific distribution, such as a standard normal distribution. This is particularly useful when the underlying data follows a particular statistical distribution assumption, as it aligns features with the expected distribution. Normalization can also be helpful when applying certain statistical tests or algorithms that make distribution assumptions.
6. Providing Stable Model Behavior: Scaling and normalization can help mitigate issues related to ill-conditioning and numerical instability. When features have significantly different scales, some algorithms may struggle to represent the data accurately and converge to stable solutions. Scaling and normalization techniques improve the numerical stability of the algorithms and ensure more stable behavior across different datasets and learning scenarios.
It is important to note that the choice of scaling and normalization techniques depends on the specific characteristics of the data and the requirements of the machine learning task. Common techniques include standardization (mean = 0, standard deviation = 1), min-max scaling to a specific range (such as [0, 1]), or more advanced methods like robust scaling or log transformations.
By scaling and normalizing feature vectors, we can create a more balanced and representative input for machine learning models. These techniques promote fair weight regularization, improve convergence speed and stability, handle outliers, and ensure consistent behavior across different datasets. Applying appropriate scaling and normalization techniques is an essential aspect of feature engineering, enhancing the performance and reliability of machine learning models.
Feature Selection Methods
Feature selection is the process of selecting a subset of relevant features from a larger set of available features. By reducing the dimensionality of the feature space, feature selection techniques aim to improve model performance, interpretability, and computational efficiency. Let’s explore some common feature selection methods:
1. Filter methods: Filter methods evaluate the relevance of features based on their statistical characteristics, such as correlation with the target variable or statistical tests like chi-square or mutual information. These methods assess the individual features independently of the machine learning algorithm. They can be computationally efficient but may disregard the relationships between features.
2. Wrapper methods: Wrapper methods evaluate the quality of feature subsets by selecting features based on their performance when used in combination with a specific machine learning algorithm. These methods involve evaluating various feature combinations using a specific performance metric, such as accuracy or area under the curve. Wrapper methods can be computationally expensive but are effective in capturing feature interactions.
3. Embedded methods: Embedded methods perform feature selection as part of the model training process. These methods include built-in feature selection techniques within machine learning algorithms, such as regularization methods like LASSO or Ridge regression. Embedded methods consider the relevance of features and their impact on the model’s performance simultaneously during the training process.
4. Recursive Feature Elimination (RFE): RFE is a wrapper-based feature selection method that recursively eliminates less informative features based on their ranking. It starts with all features and progressively removes the least significant features until a desired number of features or a specified performance threshold is reached. RFE can be used in combination with any machine learning algorithm and takes into account feature interactions.
5. Dimensionality reduction techniques: Dimensionality reduction techniques, such as principal component analysis (PCA) or linear discriminant analysis (LDA), transform the original feature space into a lower-dimensional space while retaining as much information as possible. These methods project the data onto a new set of orthogonal features that capture the most significant variations in the data. While dimensionality reduction reduces feature space, it may result in less interpretable features.
6. Tree-based feature selection: Tree-based feature selection methods use decision trees or ensemble models, such as random forests or gradient boosting, to evaluate the importance of features. These methods assess feature importance based on how often a feature is selected for splitting across multiple decision trees or how much it contributes to the overall predictive power. Tree-based feature selection can effectively handle feature interactions and non-linear relationships between features.
When choosing a feature selection method, it is important to consider the characteristics of the data, the specific requirements of the machine learning task, and the trade-off between model performance and interpretability. It is also beneficial to experiment with multiple feature selection techniques and compare their results to find the most suitable approach for a given problem.
By employing appropriate feature selection methods, we can reduce dimensionality, enhance model performance, interpret the underlying relationships between features, and improve computational efficiency. Feature selection allows us to focus on the most informative features, leading to more accurate and efficient machine learning models.
Conclusion
Feature vectors are a fundamental component of machine learning, enabling the representation and transformation of raw data into numerical representations. They capture the essential characteristics of objects or data points and serve as the input for machine learning algorithms. Creating effective feature vectors requires careful consideration of relevant features, preprocessing techniques, and feature engineering methodologies.
In this article, we explored the concept of feature vectors and their importance in machine learning. We discussed common types of features used in machine learning, such as numerical, categorical, textual, image, temporal, and geospatial features. Each type of feature provides unique information to help algorithms learn patterns and make accurate predictions.
We also delved into the feature engineering process, which involves techniques like polynomial features, scaling and normalization, one-hot encoding, handling missing data, binning, and feature extraction from text or images. These techniques aim to transform raw data into more informative and representative features for machine learning models.
Additionally, we explored the significance of scaling and normalization in feature vectors, which equalize feature magnitudes, enhance convergence speed, promote weight interpretability, handle outliers, normalize distributions, and provide stable model behavior.
Lastly, we discussed feature selection methods, including filter methods, wrapper methods, embedded methods, recursive feature elimination, tree-based feature selection, and dimensionality reduction techniques. These methods effectively reduce the dimensionality of feature space, improve model performance, interpretability, and computational efficiency.
By leveraging the concept of feature vectors and applying appropriate feature engineering techniques and feature selection methods, machine learning models can extract valuable information from data and make accurate predictions. The process of creating feature vectors requires a deep understanding of the problem domain, domain knowledge, and creativity to capture meaningful patterns and relationships.
As the field of machine learning continues to evolve, the importance of feature vectors will only grow. Investing time and effort into constructing effective feature vectors will significantly impact the performance and effectiveness of machine learning models, ultimately leading to more reliable and impactful results.