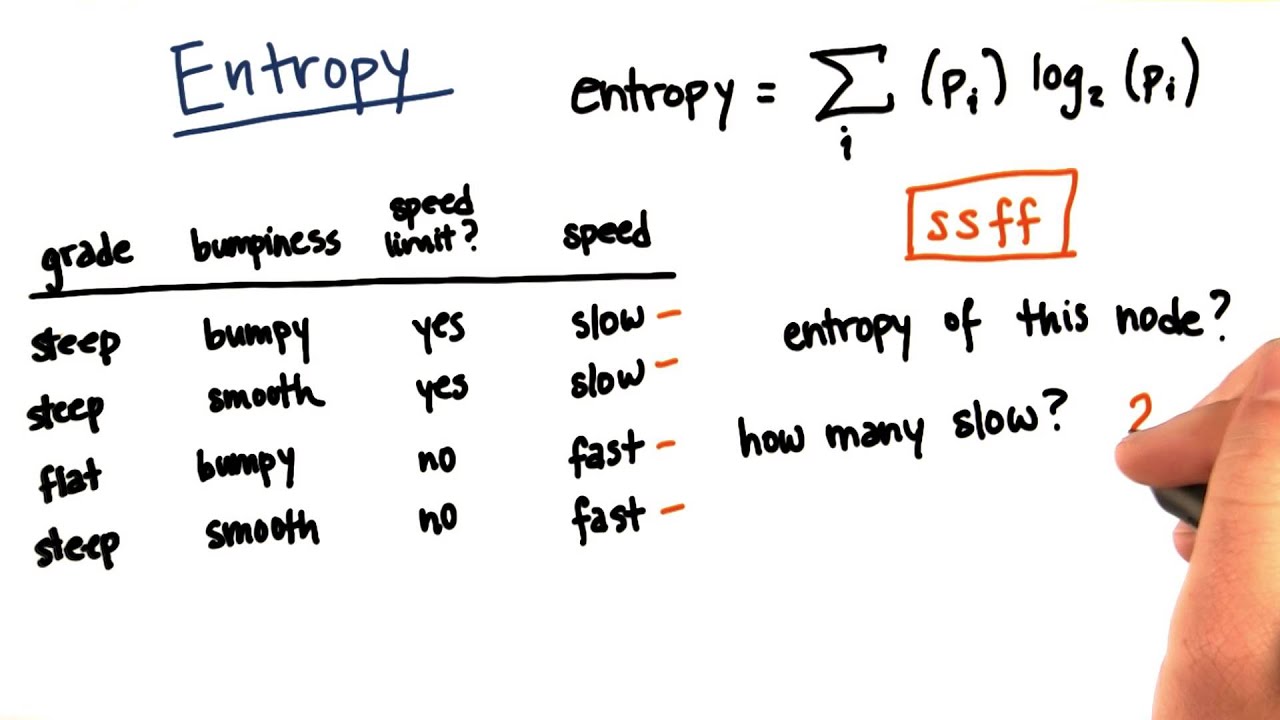What Is Entropy In Machine Learning

Introduction

Machine learning is a fascinating field that has gained significant attention and importance in recent years. As algorithms and models continue to evolve, the need to understand fundamental concepts becomes paramount. One such concept is entropy, which plays a crucial role in information theory and machine learning.

Entropy is a measure of uncertainty or randomness in a dataset. It provides insight into the amount of information or disorder within a system. While entropy finds its roots in thermodynamics, it has also found application in various fields, including machine learning.

In machine learning, entropy is utilized to measure the purity or impurity of data. It helps algorithms make decisions by evaluating the unpredictability or randomness within a given dataset. By understanding the concept of entropy, machine learning practitioners can effectively optimize models and improve decision-making processes.

Through this article, we will delve into the fundamental aspects of entropy and its applications in machine learning. We will explore how entropy is calculated, its significance as a measure of uncertainty, and its uses in determining feature importance, building decision trees, and evaluating model performance.

Whether you are new to machine learning or seeking to enhance your understanding of the topic, this article will provide valuable insights into the concept of entropy and its relevance in the field.

So, let’s begin our journey into the intriguing world of entropy in machine learning.

What Is Entropy?

In the context of information theory and machine learning, entropy is a measure of the uncertainty or randomness in a dataset. It provides a quantitative measure of how much information is needed to describe or predict the outcomes of a given system.

Entropy is often associated with the concept of disorder. In simpler terms, it represents the level of chaos or randomness within a dataset. A high entropy value indicates a high level of uncertainty and randomness, while a low entropy value signifies a more predictable and structured dataset.

To understand entropy better, let’s consider an example. Suppose you have a dataset of weather conditions in a particular city, with two possible outcomes: “rain” and “sunshine.” If, over a long period of time, it rains on half of the days and is sunny on the other half, the entropy of this dataset would be high. This is because there is an equal probability of both outcomes occurring, resulting in a higher degree of uncertainty.

On the other hand, if it is sunny on most days and rains very rarely, the entropy of the dataset would be low. This is because there is a more predictable pattern in the outcomes, reducing the level of uncertainty.

Entropy is measured using logarithmic functions, typically in base 2, which allows for easy interpretation and calculation. It is denoted by the symbol H and is often measured in bits. A bit is the basic unit of information, representing a binary choice between two possibilities.

Entropy acts as a fundamental concept in various fields, including information theory, physics, and, of course, machine learning. Its applications span across different machine learning algorithms and methodologies, where it is utilized to make informed decisions and measure the purity or impurity of data.

Now that we have a basic understanding of what entropy is, let’s explore its specific applications in the context of machine learning.

Entropy in Information Theory

Entropy is a foundational concept in information theory, a branch of mathematics that deals with the quantification and transmission of information. Developed by Claude Shannon in the 1940s, information theory provides a framework for measuring the amount of information contained in a message or signal.

In information theory, entropy is defined as the average amount of information required to encode symbols from a given source. It measures the uncertainty or randomness of the source’s output. Essentially, entropy represents the minimum number of bits required on average to encode each symbol from the source.

The entropy of a discrete random variable X with possible outcomes x₁, x₂, …, x_n and corresponding probabilities p(x₁), p(x₂), …, p(x_n) is calculated using the formula:

H(X) = – Σ [p(x_i) * log₂(p(x_i))]

Here, p(x_i) represents the probability of the i-th outcome occurring, and log₂(p(x_i)) is the binary logarithm of the probability. The negative sign in front of the sum ensures that the entropy value is always non-negative.

The entropy value is at its maximum when all outcomes in the source have equal probabilities. In this case, every outcome is equally likely, resulting in the highest level of uncertainty. On the other hand, the entropy is minimized when one outcome is certain to occur, resulting in a low level of uncertainty.

The concept of entropy in information theory has practical applications in various fields, including data compression, cryptography, and communication systems. It helps in designing efficient coding schemes, secure encryption algorithms, and optimized transmission protocols.

Now that we have explored the concept of entropy in information theory, let’s see how it is applied in the context of machine learning.

Entropy in Machine Learning

In machine learning, entropy plays a significant role in decision-making and modeling. It is commonly used as a measure of uncertainty or impurity within a dataset, allowing algorithms to make informed choices and optimize their performance.

Entropy is especially relevant in supervised learning tasks, where the goal is to learn a mapping between input features and corresponding output labels. It is often utilized in algorithms that involve decision trees and random forests.

Within the context of decision trees, entropy is used to determine the best attribute or feature to split the data. The goal is to find the feature that maximizes the reduction in entropy after the split, resulting in more homogeneous subsets and better separation of classes.

By calculating the entropy of the dataset before and after each possible split, decision tree algorithms can evaluate the information gain or reduction in uncertainty. The attribute that leads to the highest information gain is selected as the splitting criterion.

Furthermore, entropy serves as a measure of impurity in decision tree nodes. It is used to determine when to stop the tree-building process by setting a threshold on the desired purity or minimum entropy level. A node is considered pure when all examples within it belong to the same class, resulting in zero entropy and no further need for splitting.

In addition to decision trees, entropy is also used in random forests, which are ensembles of decision trees. Random forests combine multiple decision trees to make predictions and reduce overfitting. Entropy is employed to calculate the information gain at each split point and guide the tree-building process in random forests.

Furthermore, entropy can be used as a measure of the impurity or uncertainty in multi-class classification problems. It helps evaluate the distribution of different classes within a dataset and aids in determining the predictive power of different features.

Overall, entropy in machine learning acts as a valuable tool for measuring uncertainty and guiding decision-making processes. By leveraging entropy-based algorithms and methodologies, machine learning practitioners can build robust models that effectively analyze and process complex datasets.

Now that we have discussed entropy in machine learning, let’s explore how entropy is calculated and its uses in more detail.

Entropy as a Measure of Uncertainty

In the context of machine learning, entropy serves as a measure of uncertainty or impurity within a dataset. It quantifies the level of disorder or randomness in the data and provides valuable insights into the information content of the dataset.

Entropy is particularly useful in classification tasks, where the goal is to predict the class or category of an input data point. By calculating the entropy of a dataset, machine learning algorithms can estimate the amount of information required to classify an instance correctly.

When the dataset is perfectly pure or homogenous, the entropy is lowest, indicating that there is no uncertainty or randomness in the distribution of class labels. In contrast, when the dataset is completely impure or mixed, the entropy is highest, denoting a high level of uncertainty in class memberships.

Entropy provides a basis for measuring the effectiveness of splitting criteria in decision trees and random forests. The goal is to split the data based on attributes that minimize the entropy or maximize the information gain, resulting in more homogeneous subsets with clear class distinctions.

By calculating the entropy before and after a potential split, a decision tree algorithm can assess the improvement in purity or reduction in uncertainty. This information gain is an essential factor for selecting the best attribute to split the data, effectively separating the classes and improving the model’s predictive power.

Furthermore, entropy can be used to evaluate the quality of features in classification tasks. It quantifies the discriminatory power of a particular attribute in distinguishing between different classes. Features with higher entropy values contribute more information to the classification process, while features with lower entropy values may be less informative.

It is important to note that while entropy is commonly used as a measure of uncertainty, it is not the only metric available. Other alternative measures, such as Gini impurity, are also utilized in machine learning algorithms. The choice of the measure depends on the specific problem and the characteristics of the dataset.

By leveraging entropy as a measure of uncertainty, machine learning algorithms can effectively handle complex datasets, make informed decisions, and improve the accuracy of classification tasks. Understanding entropy and its role in quantifying uncertainty is fundamental to developing reliable and efficient machine learning models.

Now that we have explored entropy as a measure of uncertainty, let’s dive into the calculation of entropy and its practical applications in machine learning.

Calculating Entropy

To calculate entropy, we need to:

Determine the probabilities of each class or category in a dataset.
Calculate the logarithm of each probability.
Multiply each probability by its corresponding logarithm.
Sum up the products.
Take the negative of the sum to obtain the entropy value.

Expressed as a formula, the calculation of entropy for a given dataset is as follows:

H(X) = – Σ [p(x) * log₂(p(x))]

Where:

H(X) is the entropy of the dataset
p(x) is the probability of occurrence of class x
log₂(p(x)) is the binary logarithm of the probability
Σ denotes the sum of probabilities over all classes

The calculated entropy value will typically range from 0 to a maximum value depending on the number of classes in the dataset. A lower entropy value indicates a more predictable and structured dataset, while a higher value signifies a higher level of uncertainty and randomness.

It is important to note that the base of the logarithm used (in this case, base 2) depends on the desired unit of information. In practical terms, using base 2 allows the entropy value to be measured in bits. If natural logarithms (base e) are used, the entropy is measured in nats.

Calculating entropy plays a fundamental role in decision tree algorithms. It helps determine the information gain at each split point, enabling the identification of attributes that provide the most significant reduction in uncertainty.

By utilizing entropy calculation as a measure of dataset purity or impurity, machine learning algorithms can make informed decisions, identify relevant features, and optimize the model’s performance.

Now that we have explored how to calculate entropy, let’s move on to discuss the practical uses of entropy in machine learning.

Uses of Entropy in Machine Learning

Entropy plays a crucial role in various aspects of machine learning, offering valuable insights and aiding decision-making processes. Let’s explore some of the key uses of entropy in machine learning:

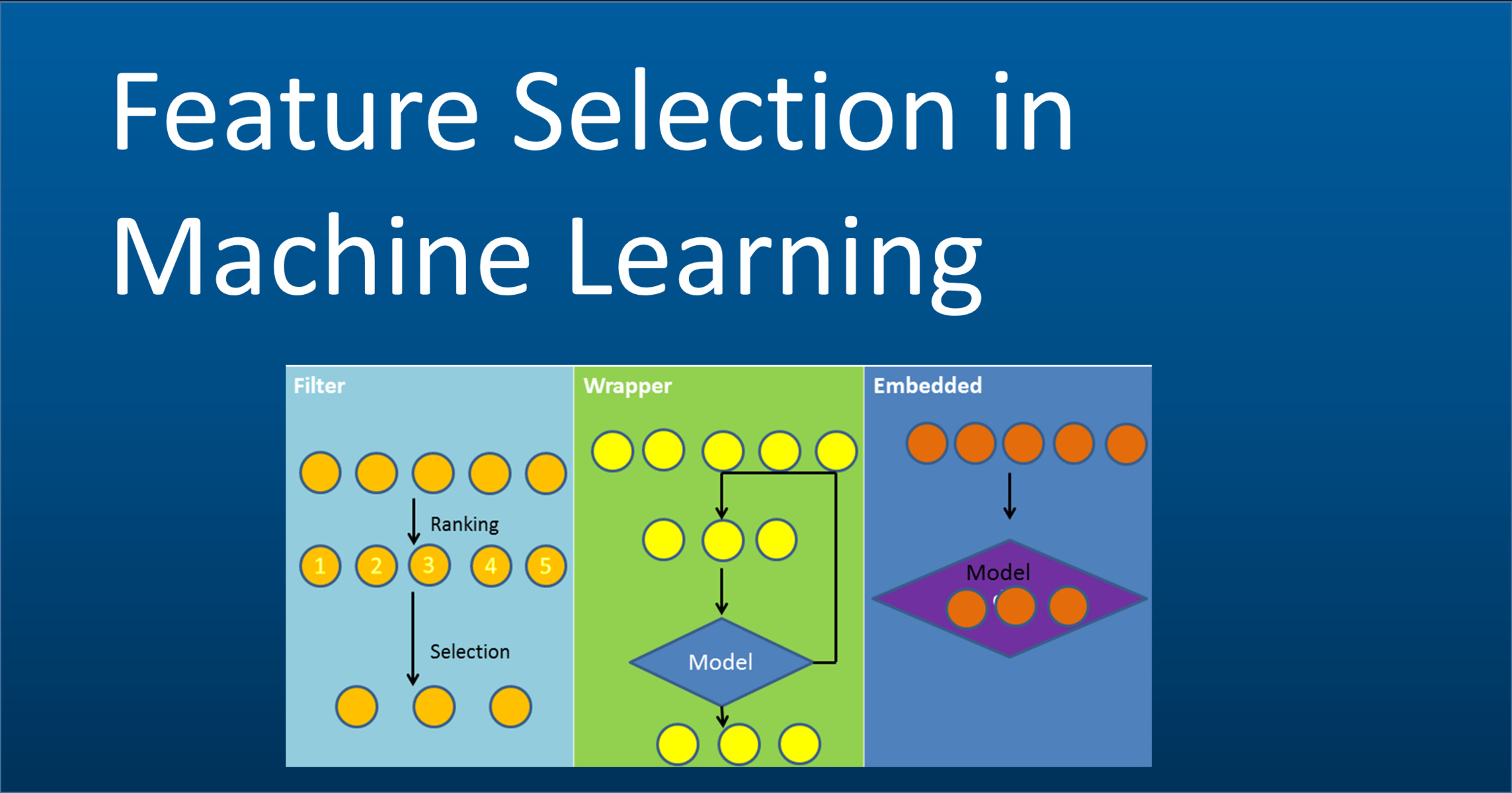
Feature Selection: Entropy is utilized to measure the importance of features in machine learning models. By calculating the entropy of a dataset before and after removing a feature, practitioners can assess the impact of the feature on the model’s predictive power. Features that result in a significant reduction in entropy when removed are considered more important for classification or regression tasks.
Splitting Criterion: Entropy is used as a criterion to decide the best attribute for splitting data in decision trees. It helps identify attributes that generate subsets with the highest information gain, leading to more accurate and efficient models. Decision tree algorithms evaluate the reduction in entropy after each possible split to determine the feature that produces the maximum information gain.
Decision Tree Pruning: Entropy is instrumental in determining when to stop the tree-growing process in decision tree algorithms. By setting a threshold on the minimum acceptable entropy or maximum tolerable impurity, decision trees can be pruned to prevent overfitting and improve generalization. Pruning ensures that the tree does not become too complex and can effectively generalize patterns from the training data to new, unseen examples.
Ensemble Methods: Entropy is used in ensemble methods like random forests, where multiple decision trees are combined to make predictions. By evaluating the information gain at each split point using entropy, random forests can effectively build diverse and accurate models.
Evaluation Metric: Entropy serves as a measure of model performance in classification tasks. Metrics such as cross-entropy loss and categorical accuracy utilize the concept of entropy to assess the discrepancy between predicted and actual class probabilities. These metrics help evaluate and compare the effectiveness of different models and guide the optimization process.

These are just a few examples of how entropy is used in machine learning. Its versatility makes it a valuable tool for data analysis, feature selection, model building, and evaluation. Understanding the concept of entropy and its practical applications enables practitioners to leverage its power and improve the effectiveness of machine learning algorithms.

Now that we have explored the uses of entropy in machine learning, let’s wrap up our discussion on this fundamental concept.

Conclusion

Entropy is a fundamental concept in machine learning that plays a crucial role in understanding uncertainty, measuring impurity, and making informed decisions. It serves as a quantitative measure of randomness and disorder within a dataset, enabling algorithms to evaluate the information content and optimize their performance.

In this article, we have explored the concept of entropy in information theory and its applications in machine learning. We have seen how entropy is calculated by determining the probabilities of different outcomes and using logarithmic functions to measure the average amount of information required for encoding.

Entropy finds practical use in various aspects of machine learning, such as feature selection, decision tree splitting, model pruning, ensemble methods, and evaluation metrics. By leveraging entropy-based algorithms and methodologies, machine learning practitioners can build robust models, handle complex datasets, and improve the prediction accuracy.

Understanding and incorporating entropy in machine learning allows for better decision-making, improved model performance, and more efficient data analysis. It is a versatile tool that aids in capturing the inherent uncertainty and randomness present in real-world problems.

As the field of machine learning continues to advance, a solid grasp of concepts like entropy becomes increasingly important. By delving into the intricacies of entropy, machine learning practitioners can enhance their understanding of algorithms, optimize their model designs, and tackle a wide range of predictive tasks.

In conclusion, entropy serves as a valuable measure of uncertainty in machine learning. Its applications span across multiple domains, and its integration into machine learning algorithms can significantly enhance the performance and accuracy of models. By embracing the concept of entropy, practitioners can unlock the full potential of their machine learning endeavors.